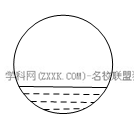
题目内容
如图, 为
为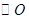 的切线,
的切线,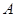 为切点,
为切点,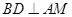 于点
于点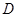 ,
,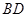 交
交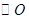 于
于 ,平分
,平分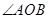 .求
.求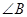 的度数.
的度数.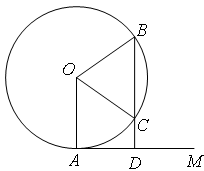
 为
为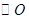 的切线,
的切线,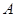 为切点,
为切点,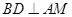 于点
于点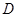 ,
,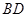 交
交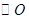 于
于 ,平分
,平分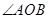 .求
.求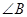 的度数.
的度数.
60°
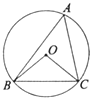
分析:由于AM是切线,BD⊥AM,易得∠OAM=∠BDM=90°,从而可证OA∥BD,那么就有∠AOC=∠BCO,OC是∠AOB角平分线,易得∠AOC=∠BOC,可得∠BOC=∠BCO,又OB=OC,从而可证明△OBC是等边三角形,从而可求∠B。
解答:
∵AM是切线,
∴OA⊥AM,
∴∠OAM=90°,
又∵BD⊥AM,
∴∠BDM=90°,
∴∠OAM=∠BDM,
∴AO∥BD,
∴∠AOC=∠BCO,
∵OC是∠AOB平分线,
∴∠AOC=∠BOC,
∴∠BOC=∠BCO,
又∵OB=OC,
∴∠OBC=∠OCB,
∴△OBC为等边三角形,
∴∠B=60°。
点评:本题考查了切线的性质、平行线的判定和性质、角平分线的概念,难度一般,解答本题的关键是证明OA∥BD。

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
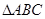 中,
中,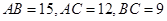 ,经过点
,经过点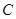 且与边
且与边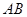 相切的动圆与
相切的动圆与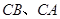 分别相交于点
分别相交于点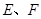 ,则线段
,则线段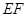 长度的最小值()
长度的最小值()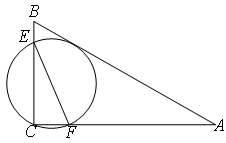
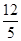

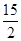
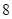
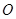 的半径长为
的半径长为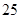 ,弦
,弦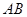 长为
长为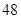 ,
,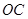 平分
平分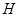 .交
.交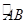 于点
于点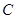 ,求
,求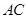 的长
的长