题目内容
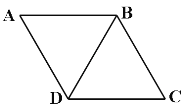
【题目】在菱形ABCD中,BD=BC,
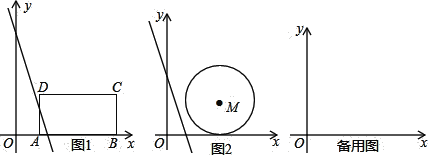
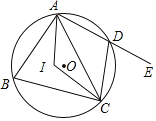
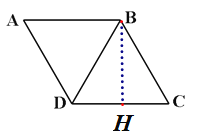
(1)如图,若菱形ABCD的面积为6![]() .求点B到DC的最短距离.
.求点B到DC的最短距离.
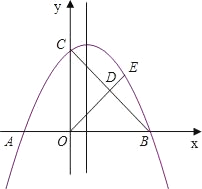
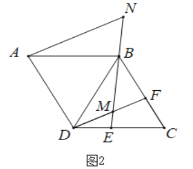
(2)如图2,点F在BC边上,且DE=CF,连接DF交BE于点M,连接EB并延长至点N,使得BN=DM,求证:AN=DM+BM.
【答案】(1)3(2)证明见解析
【解析】
(1)由四边形ABCD为菱形及BD=CD,可知![]() 是等边三角形,由垂线段的性质知当BH
是等边三角形,由垂线段的性质知当BH![]() 时,点B到CD的距离最短.然后根据等边三角形的性质及面积法即可求出点B到CD的最短距离为3 ;
时,点B到CD的距离最短.然后根据等边三角形的性质及面积法即可求出点B到CD的最短距离为3 ;
(2)如图2中,连接AM,在MA上截取MH=MD,连接DH.想办法证明△AMN,△DMH都是等边三角形,△ADH≌△BDM即可解决问题;
(1)解:∵四边形ABCD为菱形,
∴BC=CD 又∵BD=CD,
∴![]() ,
,
当BH![]() 时,点B到CD的距离最短。
时,点B到CD的距离最短。
∵![]() ,且BH
,且BH![]() ,
,
∴H为CD中点,设CD=2x.则BH=![]() ,
,
∴![]() , 解得
, 解得![]() ,
,
∴BH=3,即点B到CD的最短距离为3 ;
(2)连接AM,
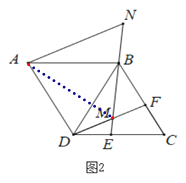
∵DE=CF.∠BDE=∠C,BD=CD,
∴△BDE≌△DCF,
∴∠DBE=∠CDF,
∴∠BMF=∠DBM+∠BDM=∠CDF+∠BDM=60°,
∴∠DMB=120°,
∵∠DAB+∠DMB=180°,
∴∠ADM+∠ABM=180°,
又∵∠ABN+∠ABM=180°,
∴∠ABN=∠ADM,
∵AB=AD,BN=DM,
∴△ABN≌△ADM,
∴∠DAM=∠BAN,AM=AN,
∴∠MAN=∠DAB=60°,
∴△AMN是等边三角形,
∴AN=NM,
又∵NM=NB+BM,NB=DM,
∴AN=DM+BM.

练习册系列答案
相关题目