题目内容
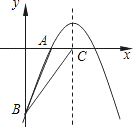
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=﹣2x+2的图象.

(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.
【答案】(1)A(﹣1,0),(1,0),P(![]() ,
,![]() ).(2)四边形PQOB的面积=
).(2)四边形PQOB的面积= ![]() .
.
【解析】
试题分析:(1)令一次函数y=x+1与一次函数y=﹣2x+2的y=0可分别求出A,B的坐标,再由![]() 可求出点P的坐标;
可求出点P的坐标;
(2)根据四边形PQOB的面积=S△BOM﹣S△QPM即可求解.
解:(1)∵一次函数y=x+1的图象与x轴交于点A,∴A(﹣1,0),
一次函数y=﹣2x+2的图象与x轴交于点B,∴B(1,0),
由![]() ,解得
,解得![]() ,∴P(
,∴P(![]() ,
,![]() ).
).
(2)设直线PA与y轴交于点Q,则Q(0,1),直线PB与y轴交于点M,则M(0,2),
∴四边形PQOB的面积=S△BOM﹣S△QPM=![]() ×1×2﹣
×1×2﹣![]() ×1×
×1×![]() =
=![]() .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目