题目内容
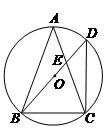
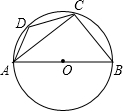
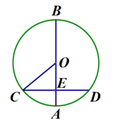
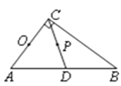
如图,点A、E,是半圆周上的三等分点,直径=2, ,垂足为,连接交于,过作∥交于.
,垂足为,连接交于,过作∥交于.

(1)判断直线与⊙的位置关系,并说明理由.
(2)求线段的长.
 ,垂足为,连接交于,过作∥交于.
,垂足为,连接交于,过作∥交于.
(1)判断直线与⊙的位置关系,并说明理由.
(2)求线段的长.
(1)直线AG与⊙O的位置关系是AG与⊙O相切,理由见解析;(2)AF的长是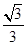 .
.
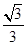 .
.试题分析:(1)求出弧AB=弧AE=弧EC,推出OA⊥BE,根据AG∥BE,推出OA⊥AG,根据切线的判定即可得出答案;
(2)求出等边三角形AOB,求出BD、AD长,求出∠EBC=30°,在△FBD中,通过解直角三角形求出DF即可.
试题解析:(1)直线AG与⊙O的位置关系是AG与⊙O相切,
理由是:连接OA,
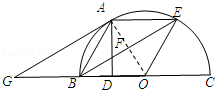
∵点A,E是半圆周上的三等分点,
∴弧AB=弧AE=弧EC,
∴点A是弧BE的中点,
∴OA⊥BE,
又∵AG∥BE,
∴OA⊥AG,
∴AG与⊙O相切;
(2)∵点A,E是半圆周上的三等分点,
∴∠AOB=∠AOE=∠EOC=60°,
又∵OA=OB,
∴△ABO为正三角形,
又∵AD⊥OB,OB=1,
∴BD=OD=
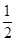 ,AD=
,AD=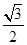 ,
,又∵∠EBC=
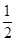 ∠EOC=30°(圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半),
∠EOC=30°(圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半),在Rt△FBD中,FD=BD•tan∠EBC=BD•tan30°=
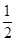 ×
×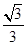 =
=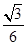 ,
,∴AF=AD﹣DF=
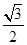 ﹣
﹣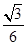 =
=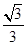 .
.答:AF的长是
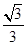 .
.考点:1.切线的判定,2.等边三角形的判定与性质,3.垂径定理.

练习册系列答案
相关题目
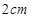 的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“
的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“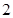 ”和“
”和“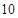 ”(单位:
”(单位: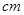 ),那么该光盘的直径为
),那么该光盘的直径为 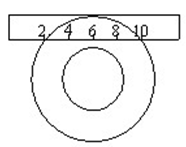

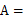 50°,∠
50°,∠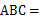 60°,
60°,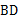 是圆
是圆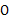 的直径,
的直径,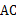 于点
于点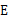 ,连结
,连结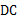 ,则∠
,则∠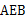 等于( )
等于( )