题目内容
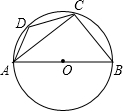
如图，已知AB是⊙O的直径，C、D是⊙O上两点．且∠D=130°．则∠BAC的度数是_________
40°．
试题分析：根据圆周角定理，由AB是⊙O的直径，可证∠ACB=90°，由圆内接四边形的对角互补可求∠B=180°-∠D=50°，即可求∠BAC=90°-∠B=40°．
试题解析：∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠B=180°-∠D=50°，
∴∠BAC=90°-∠B=40°．
考点: 1.圆周角定理；2.圆内接四边形的性质.
练习册系列答案
相关题目
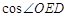的值．
,垂足为,连接交于,过作∥交于．
中,⊙A与y轴相切于点
,与x轴相交于M、N两点.如果点M的坐标为
,求点N的坐标.
