Question

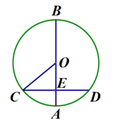
如图，AB为⊙O的直径，弦CD^AB，垂足为点E，连接OC，若OC=5，AE=2，则CD等于

A．3

B．4

C．6

D．8

Answer 1

D.

试题分析：先根据AB为圆O的直径，弦CD⊥AB可知CD=2CE，再根据OC=5，AE=2可求出OE的长，利用勾股定理可求出CE的长，进而可求出答案．
∵AB为圆O的直径，弦CD⊥AB，
∴CD=2CE，
∵OC=5，AE=2，
∴OA=5，
∴OE=OA-AE=5-2=3，
∴CE=
∴CD=2CE=8
故选D．
考点:1. 垂径定理；2.勾股定理．