题目内容
【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°. △ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.

【答案】(1)AD=AE,证明见解析;(2)成立,证明见解析.
【解析】试题分析: (1)由等边三角形的性质得到∠B=∠ACE=60°,AB=AC,再有∠DAB=∠EAC可证明△ABD≌△ACE即可得到结论;
(2)由等边三角形的性质得到∠ABD=∠ACE=120°,AB=AC,再有∠DAB=∠EAC可证明△ABD≌△ACE即可得到结论.
试题解析:
(1)结论:AD=AE,理由如下:
∵△ABC是等边三角形,
∴∠B=∠ACE=60°,AB=AC
∵∠DAE=60°,CE平分∠ACF,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴AD=AE;
(2)如图所示,
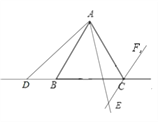
∵△ABC是等边三角形,
∴∠ABD =120°,AB=AC,
∵CF平分△ABC的外角,
∴∠ACE=120°
∴∠ABD=∠ACE
∵∠DAE=∠BAC=60°
∴∠DAB=∠EAC
∴△ABD≌△ACE,
∴AD=AE.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目






