题目内容
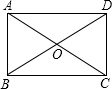 如图所示,四边形ABCD的对角线AC,BD交于点O.下列条件中,可判定四边形ABCD为矩形的是
如图所示,四边形ABCD的对角线AC,BD交于点O.下列条件中,可判定四边形ABCD为矩形的是
- A.AC=BD
- B.△AOB是等边三角形
- C.AO=CO=BO=DO
- D.∠ABC+∠BCD+∠CDA+∠DAB=360°
C
分析:根据矩形的性质可知矩形的对角线平分且相等可得AO=CO=BO=DO,故求解.
解答:A、对角线互相平分且相等的四边形是矩形,故不能;
B、△AOB是等边三角形不能判定四边形ABCD为矩形;
C、对角线互相平分且相等的四边形是矩形,故能判定;
D、四边形的内角和是360°,故不能.
故选C.
点评:矩形的判定定理有:
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线互相平分且相等的四边形是矩形.
分析:根据矩形的性质可知矩形的对角线平分且相等可得AO=CO=BO=DO,故求解.
解答:A、对角线互相平分且相等的四边形是矩形,故不能;
B、△AOB是等边三角形不能判定四边形ABCD为矩形;
C、对角线互相平分且相等的四边形是矩形,故能判定;
D、四边形的内角和是360°,故不能.
故选C.
点评:矩形的判定定理有:
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线互相平分且相等的四边形是矩形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
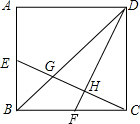
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )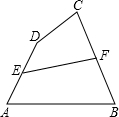 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.