题目内容
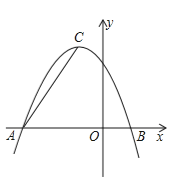
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别是
轴的两个交点分别是![]() 、
、![]() ,
,![]() 为顶点.
为顶点.
(1)求![]() 、
、![]() 的值和顶点
的值和顶点![]() 的坐标;
的坐标;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为斜边的直角三角形?若存在,求出点
为斜边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ,(-1,4);(2)在y轴上存在点D (0,3)或D (0,1),使△ACD是以AC为斜边的直角三角形
,(-1,4);(2)在y轴上存在点D (0,3)或D (0,1),使△ACD是以AC为斜边的直角三角形
【解析】
(1)把A(-3,0),B(1,0)代入![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)过C作CE⊥y轴于E,根据函数的解析式求得C(-1,4),得到CE=1,OE=4,设![]() ,得到
,得到![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
(1)把A(3,0)、B(1,0)分别代入![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
则该抛物线的解析式为:![]() ,
,
∵![]() ,
,
所以顶点![]() 的坐标为(
的坐标为(![]() ,
,![]() );
);
故答案为:![]() ,
,![]() ,顶点
,顶点![]() 的坐标为(
的坐标为(![]() ,
,![]() );
);
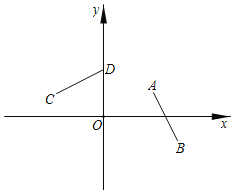
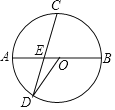
(2)如图1,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,
,

假设在![]() 轴上存在满足条件的点
轴上存在满足条件的点![]() ,
,
设![]() (0,
(0,![]() ),则
),则![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由∠![]() 90
90![]() 得∠1
得∠1![]() ∠2
∠2![]() 90
90![]() ,
,
又∵∠2![]() ∠3
∠3![]() 90
90![]() ,
,
∴∠3![]() ∠1,
∠1,
又∵∠CED![]() ∠DOA
∠DOA![]() 90
90![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
则![]() ,
,
变形得![]() ,
,
解得![]() ,
,![]() .
.
综合上述:在y轴上存在点![]() (0,3)或
(0,3)或![]() (0,1),使△ACD是以AC为斜边的直角三角形.
(0,1),使△ACD是以AC为斜边的直角三角形.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目