题目内容
【题目】如图,平面直角坐标系xOy中,A(2,1),B(3,﹣1),C(﹣2,1),D(0,2).已知线段AB绕着点P逆时针旋转得到线段CD,其中C是点A的对应点.
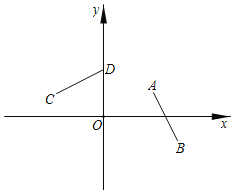
(1)用尺规作图的方法确定旋转中心P,并直接写出点P的坐标;(要求保留作图痕迹,不写作法)
(2)若以P为圆心的圆与直线CD相切,求⊙P的半径
【答案】(1)如图点P即为所求.见解析;(2)以P为圆心的圆与直线CD相切,⊙P的半径为![]() .
.
【解析】
(1)作相对AC,BD的垂直平分线,两条垂直平分线的交点P即为所求.
(2)作PE⊥CD于E,求出点E的坐标,利用相似三角形的性质求出PE即可.
(1)如图点P即为所求.
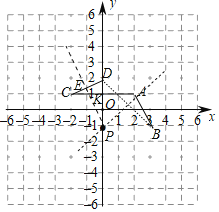
(2)作PE⊥CD于E,设AC交PD于K.
∵∠CDO=∠PDE,∠CKD=∠PED=90°,
∴△COD∽△PED,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PE=![]() ,
,
∵以P为圆心的圆与直线CD相切,
∴⊙P的半径为![]() .
.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用 (元) | ||
A | B | ||
第一次 | 20 | 50 | 4100 |
第二次 | 30 | 40 | 3700 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件50元出售,
商品以每件50元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的
商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.