题目内容
【题目】分类是研究问题的一种常用方法,我们在学习有理数和代数式的相关概念、运算法则时,除了 学到了具体知识,还学会了分类思考,在进行分类时,我们首先应明确分类标准,其次要做到分类时既不 重复,也不遗漏。
(初步感受)(1)在对多项式![]() ,
,![]() 进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
(简单运用)(2)已知 a, b 是有理数,比较 a b 与 a b的大小;
(深入思考)(3)已知 a, b c 是有理数,且 ca b>ca b ,判断 b, c 的符号,并说明理由。
【答案】(1)按项数分,分为 2 类,按次数分,分为 2 类;
(2)① ![]() 时,
时, ![]()
② ![]() 时,
时, ![]()
③ ![]() 时,
时, ![]()
(3) b,c同正或同负
【解析】
(1)可按照项数分类为二项式和三项式,按照次数分类为一次多项式和二次多项式即可;
(2)运用作差法![]() ,故只需要考虑b的取值即可判断大小;
,故只需要考虑b的取值即可判断大小;
(3)分类讨论:①![]() ;②
;②![]() ;③
;③![]() 三种情况讨论,即可得到c的取值范围,即可判断b、c的符号;或者直接计算解不等式分析即可.
三种情况讨论,即可得到c的取值范围,即可判断b、c的符号;或者直接计算解不等式分析即可.
解:(1)按项数分,分为 2 类
二项式:![]()
三项式: ![]()
按次数分,分为 2 类
一次多项式:![]()
二次多项式: ![]()
(2)![]()
① ![]() 时,
时,![]() ,∴
,∴![]()
② ![]() 时,
时,![]() ,∴
,∴![]()
③ ![]() 时,
时, ![]() ,∴
,∴![]()
(3)法一:解:①![]() 时 ,
时 , ![]() ,此时
,此时 ![]() (舍)
(舍)
②![]() 时 ,
时 ,
![]()
∵![]()
∴![]()
③b<0时,
![]()
![]()
![]()
综上: b,c同正或同负
法二:解:![]() ,
,
整理得:
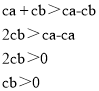
∴c、b同正或同负

练习册系列答案
相关题目
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.