��Ŀ����
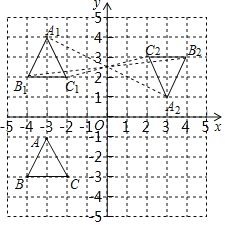
����Ŀ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-3-1����B��-4��-3����C��-2��-3����
��1����������ABC����ƽ��5����λ�õ�����A1B1C1����д����B1�����ꣻ
��2��������ABC���ڵ�O�����ĶԳƵ�ͼ����A2B2C2����д����B2�����ꣻ
��3���۲�ͼ�Σ���A1B1C1����A2B2C2�����ĶԳ�����������ĶԳƣ���ô�Գ����ĵ�����Ϊ_____������������ĶԳƣ���˵�����ɣ�

���𰸡���1����A1B1C1��Ϊ������������B1������Ϊ��-4��2������2����A2B2C2��Ϊ������������B2������Ϊ��4��3������3����0��2.5����
��������
��1�����������ƽ�Ƶ����ʻ�����������ABC����ƽ��5����λ�õ�����A1B1C1��Ȼ������ƽ�ƹ���д����B1�����ꣻ
��2��������������ĶԳƵ����ʻ�����ABC���ڵ�O�����ĶԳƵ�ͼ����A2B2C2��Ȼ���������ĶԳƹ���д����B2�����ꣻ
��3���������ĶԳƵ����ʼ�����⣮
�⣺��1����A1B1C1��Ϊ����B1������Ϊ��-4��2����
��2����A2B2C2������B2��������4��3����
��3����A1B1C1����A2B2C2�����ĶԳ��𣬶Գ����ĵ�����Ϊ��0��2.5����
�ʴ�Ϊ����0��2.5����

 ������ϵ�д�
������ϵ�д�