题目内容
【题目】观察下面各图,寻找对顶角(不含平角)
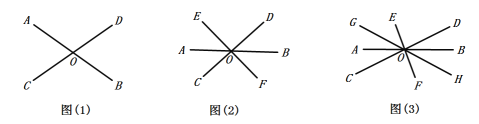
(1)如图(1),图中共有________对不同的对顶角.
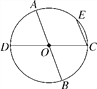
(2)如图(2),图中共有________对不同的对顶角.
(3)如图(3),图中共有________对不同的对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有![]()
![]() 条直线相交于一点,则可形成________对不同的对顶角.
条直线相交于一点,则可形成________对不同的对顶角.
(5)计算2013条直线相交于一点,则可形成________对不同的对顶角.
【答案】2 6 12 ![]() 4050156
4050156
【解析】
(1)根据对顶角的定义,写出所有不同的对顶角即可得出结论;
(2)根据对顶角的定义,写出所有不同的对顶角即可得出结论;
(3)根据对顶角的定义,写出所有不同的对顶角即可得出结论;
(4)根据(1)(2)(3)的规律,总结出公式即可;
(5)将![]() 代入(4)中公式计算即可.
代入(4)中公式计算即可.
解:(1)对顶角有:∠AOC和∠BOD,∠AOD和∠BOC,
共有2对不同的对顶角
故答案为2;
(2)对顶角有:∠AOC和∠BOD,∠AOE和∠BOF、∠COF和∠EOD,∠AOD和∠BOC,∠BOE和∠AOF,∠COE和∠DOF
共有6对不同的对顶角
故答案为6;
(3)对顶角有:∠AOC和∠BOD,∠COF和∠EOD,∠FOH和∠EOG、∠BOH和∠AOG、∠AOE和∠BOF、∠GOD和∠COH,∠EOB和∠AOF,∠DOH和∠COG,∠AOD和∠BOC,∠COE和∠DOF,∠FOG和∠EOH、∠AOH和∠GOB,
共有12对不同的对顶角
故答案为12;
(4)两条直线相交,共有2=2×1对不同的对顶角;
三条直线相交,共有6=3×2对不同的对顶角;
四条直线相交,共有12=4×3对不同的对顶角;
∴有![]()
![]() 条直线相交时,有
条直线相交时,有![]() 对不同的对顶角
对不同的对顶角
故答案为:![]() ;
;
(5)当![]() 时,可形成
时,可形成![]() (对)不同的对顶角
(对)不同的对顶角
故答案为:4050156.