Question

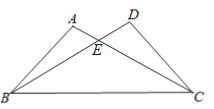
【题目】已知：如图，AD=AE，∠B=∠C，∠BAE=∠CAD，BD与CE相于点F．

求证：（1）AB=AC；（2）FB=FC．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

可以根据题目所给的条件求出△ABD≌△ACE，即可得出答案；连接BC，运用等量关系∠ABC–∠ABD=∠ACB–∠ACE即可求得答案.

证明：（1）∵∠BAE=∠CAD（已知），

∴∠BAE+∠EAD=∠CAD+∠DAE（等式性质），即∠BAD=∠CAE．1分

在△ABD和△ACE中，

∴△ABD≌△ACE（A.A.S）．

∴AB=AC（全等三角形对应边相等）．

(2) 联结BC．

∵AB=AC（已证）,

∴∠ABC=∠ACB(等边对等角)．

∵∠ABD=∠ACE　(已证),

∴∠ABC–∠ABD=∠ACB–∠ACE（等式性质），即∠FBC=∠FCB．

∴FB=FC (等角对等边)．