ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕуAЁЂBЁЂCдкЭЌвЛжБЯпЩЯЃЌAB=2ЃЌBC=1ЃЌЗжБ№вдABЁЂBCЮЊБпЃЌдкACЭЌВрзїЕШБпЁїABDКЭЕШБпЁїBCEЃЌЗжБ№СЊНсAEЁЂCD.
ЃЈ1ЃЉевГіЭМжаЕФШЋЕШШ§НЧаЮЃЈВЛЬэМгИЈжњЯпЃЉЃЌВЂжЄУїФуЕФНсТл.

(2)ЯпЖЮAEгыЯпЖЮCDЕФЙиЯЕЪЧЃКAE CDЃЈЬю>ЁЂ=ЁЂ<ЃЉ.AEгыCDЕФМаНЧЪЧЃК .
(3) ЁїABDЙЬЖЈВЛЖЏЃЌЪЙЁїBCEШЦзХЕуBа§зЊЃЌЂйетЪБЃЈ2ЃЉЕУГіЕФНсТлЛЙГЩСЂТ№ЃЈВЛвЊЧѓжЄУїЃЉЃП
Ђкдка§зЊЙ§ГЬжаЃЌЯпЖЮDCЕФГЄЪЧБфЛЏЕФЃЌЫќЕФБфЛЏЗЖЮЇЪЧ .
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтПЩЕУЁїABEЁеЁїDBCЃЛ
ЃЈ2ЃЉгЩЁїABEЁеЁїDBCЕУЃЌAE=CD, ЁЯBAE=ЁЯBDCЃЌЁЯBDC+ЁЯBCD=180Ёу-60Ёу-60Ёу=60ЁуЃЌЙЪПЩЕУAEгыCDЕФМаНЧЮЊЁЯBAE+ЁЯBCD=ЁЯBDC+ЁЯBCD=60ЁуЃЛ
ЃЈ3ЃЉЂйГЩСЂЃЛ
ЂкЕБBCдкDBЩЯЪБЃЌDCзюЖЬЕШгк1ЃЛЕБBCдкDBЕФбгГЄЯпЩЯЪБЃЌDCзюГЄЕШгк3ЃЌДгЖјПЩЕУНсТл.
ЃЈ1ЃЉ![]() ЃЌ
ЃЌ
жЄУїЃК![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
![]() ЃЌ
ЃЌ
![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
![]()
![]()
МД![]()
дк![]() КЭ
КЭ![]() жа
жа
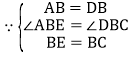
![]()
(2)ЯпЖЮAEгыЯпЖЮCDЕФЙиЯЕЪЧЃКAE=CDЃЛAEгыCDЕФМаНЧЪЧЃК![]() .
.
(3) Ђй ЃЈ2ЃЉЕУГіЕФНсТлШдГЩСЂ.
Ђк дка§зЊЙ§ГЬжаЃЌЯпЖЮDCЕФГЄЪЧБфЛЏЕФЃЌЫќЕФБфЛЏЗЖЮЇЪЧ![]() .
.

 ПкЫуФмЪжЯЕСаД№АИ
ПкЫуФмЪжЯЕСаД№АИ




