题目内容
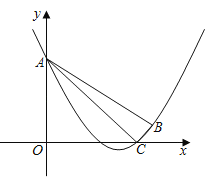
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+5,点A坐标为(0,5);(2)详见解析;(3)
x+5,点A坐标为(0,5);(2)详见解析;(3)![]() .
.
【解析】
(1)将点B、C代入抛物线解析式y=![]() x2+mx+n即可;
x2+mx+n即可;
(2)先证△ABC为直角三角形,再证∠QAP+∠CAB=90°,又因∠AQP=∠ACB=90°,即可证△PQA∽△ACB;
(3)做点B关于AC的对称点B',求出BB'的坐标,直线AB'的解析式,即可求出点F'的坐标,接着求直线FF'的解析式,求出其与AB的交点即可.
解:(1)将B(6,1),C(5,0)代入抛物线解析式y=![]() x2+mx+n,
x2+mx+n,
得
解得,m=﹣![]() ,n=5,
,n=5,
则抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x+5,点A坐标为(0,5);
x+5,点A坐标为(0,5);
(2)∵AC=![]() ,BC=
,BC=![]() ,AB=
,AB=![]() ,
,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠ACB=90°,
当∠PAB=45°时,点P只能在点B右侧,过点P作PQ⊥y 轴于点Q,
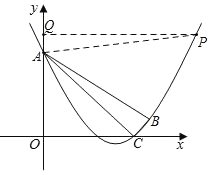
∴∠QAB+∠OAB=180°﹣∠PAB=135°,
∴∠QAP+∠CAB=135°﹣∠OAC=90°,
∵∠QAP+∠QPA=90°,∴∠QPA=∠CAB,
又∵∠AQP=∠ACB=90°,∴△PQA∽△ACB;
(3)做点B关于AC的对称点B',则A,F',B'三点共线,
由于AC⊥BC,根据对称性知点B'(4,﹣1),
将B'(4,﹣1)代入直线y=kx+5,
∴k=﹣![]() ,∴yAB'=﹣
,∴yAB'=﹣![]() x+5,
x+5,
联立 解得,x1=
解得,x1=![]() ,x2=0(舍去),
,x2=0(舍去),
则F'(![]() ,﹣
,﹣![]() ),
),
将B(6,1),B'(4,﹣1)代入直线y=mx+n,
得,![]() 解得,
解得,![]() ∴yBB'=x﹣5,
∴yBB'=x﹣5,
由题意知,kFF'=KBB',∴设yFF'=x+b,
将点F'(![]() ,﹣
,﹣![]() )代入,得,b=﹣
)代入,得,b=﹣![]() ,
,
∴yFF'=x﹣![]() ,
,
联立 解得,
解得,
∴F(![]() ,
,![]() ),
),
则FF'=![]() =
=![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间具有某种函数关系,其对应规律如下表所示
售价x(元/本) | … | 22 | 23 | 24 | 25 | 26 | 27 | … |
销售量y(件) | … | 36 | 34 | 32 | 30 | 28 | 26 | … |
(1)请直接写出y与x的函数关系式: .
(2)设该文店每周销售这种纪念册所获得的利润为W元,写出W与x之间的函数关系式,并求出该纪念册的销售单价定为多少元时,才能使文具店销售该纪念册每周所获利润最大?最大利润是多少?