Question

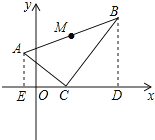
【题目】如图，已知ΔABC在坐标平面内的顶点C（2，0），∠ACB＝90°，∠B＝30°，AB＝6，∠BCD＝45°。①求A、B的坐标；②求AB中点M的坐标.

Answer 1

【答案】①A点坐标为（-1，3），B点坐标（2+3，3）；②AB中点M点坐标为（，）

【解析】分析：①过A作AE⊥x轴于点E，过B作BD⊥x轴于点D，先解直角△ABC，得到AC=AB=3，BC=AC=3，再由△BCD是等腰直角三角形得出CD=BD=BC=3，由△ACE是等腰直角三角形得出AE=CE=AC=3, 再根据C的坐标为（2，0），即可求出A、B的坐标；

②由A、B两点的坐标，根据中点坐标公式即可求出AB中点M的坐标.

详解：

①过A作AE⊥x轴于点E，过B作BD⊥x轴于点D．

在△ABC中，∵∠ACB=90°，∠B=30°，AB=6，

∴AC=AB=3，BC=AC=3．

在△BCD中，∵∠BDC=90°，∠BCD=45°，

∴∠BCD=45°，

∴CD=BD=BC=3．

在△ACE中，∵∠AEC=90°，∠ACE=45°，

∴AE=CE=AC=3．

∵C（2，0），

∴OC=2，

∴OE=CE-OC=1，

∴A点坐标为（-1，3）．

∵OD=OC+CD=2+3,

∴B点坐标（2+3，3）

②A点坐标为（-1，3），B点坐标（2+3，3），

∴AB中点M点坐标为（，）