题目内容
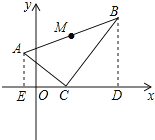
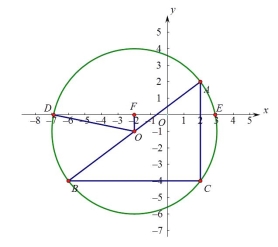
【题目】平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4).则△ABC的外接圆的圆心坐标为 , △ABC的外接圆在x轴上所截的弦长为 .
【答案】(-2,-1);![]()
【解析】在平面直角坐标中标出点A(2,2),B(-6,-4),C(2,-4),
可得![]() ABC是一个直角三角形,
ABC是一个直角三角形,
所以![]() ABC的外心O是AB的中点,则外心O的坐标为
ABC的外心O是AB的中点,则外心O的坐标为![]() , 即(-2,-1);
, 即(-2,-1);![]()
![]() 作OF
作OF![]() x轴,则外心到x轴的距离是OF=1,且
x轴,则外心到x轴的距离是OF=1,且![]() ABC的外接圆半径为
ABC的外接圆半径为![]() ,
,
则弦长DE=2×![]() .
.
所以答案是(-2,-1);4 ![]() .
.
【考点精析】本题主要考查了圆心角、弧、弦的关系和三角形的外接圆与外心的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目