题目内容
【题目】如图,点E,F分别在x轴,y轴的正半轴上.点![]() 在线段EF上,过A作
在线段EF上,过A作![]() 分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作
分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作![]() ,交CP的延长线于点G,交CA的延长线于点D.有以下结论①
,交CP的延长线于点G,交CA的延长线于点D.有以下结论①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的结论是_____.(写出所有正确结论的番号)
,其中正确的结论是_____.(写出所有正确结论的番号)

【答案】①③④.
【解析】
如图,作AM⊥y轴于M,AN⊥OE于N.首先证明四边形AMON是正方形,再证明△AMF≌△ANB(ASA),△AMC≌△ANE(ASA),△AFC≌△ABE(SSS)即可解决问题.
解:如图,作AM⊥y轴于M,AN⊥OE于N.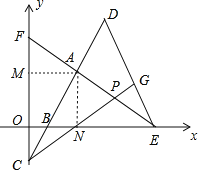
∵A(4,4),
∴AM=AN=4,
∵∠AMO=∠ONA=90°,
∴四边形ANON是矩形,
∵AM=AN,
∴四边形AMON是正方形,
∴OM=ON=4,
∴∠MAN=90°,
∵CD⊥EF,
∴∠FAC=∠MAN=90°,
∴△AMF≌△ANB(ASA),∴FM=BN,
∴OF+OB=OM+FM+ON-BN=2OM=8,故③正确,
同法可证△AMC≌△ANE(ASA),
∴CM=NE,AC=AE,故①正确;
∵FM=BN,
∴CF=BE,
∵AC=AE,AF=AB,
∴△AFC≌△ABE(SSS),
∴S△ABE-S△BOC=S△AFC-S△BOC=S四边形ABOF=S正方形AMON=16,故④正确,
当BE为定值时,点P是动点,故PC≠BE,故②错误,
故答案为①③④.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.