题目内容
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]()
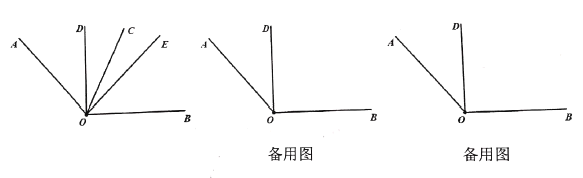
(1)求![]() ;
;
(2)![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转
的速度逆时针方向旋转![]() 秒(
秒(![]() ),
),![]() 为何值时
为何值时![]() ;
;
(3)射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转,射线
的速度逆时针方向旋转,射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度顺时针方向旋转,若射线
的速度顺时针方向旋转,若射线![]() 同时开始旋转
同时开始旋转![]() 秒(
秒(![]() )后得到
)后得到![]() ,求
,求![]() 的值.
的值.
【答案】(1)∠COE =20°;(2)当![]() =11时,
=11时,![]() ;(3)m=
;(3)m=![]() 或
或![]()
【解析】
(1)根据角平分线的定义和垂直定义即可求出∠BOD=90°,∠BOE=∠DOE =45°,即可求出∠AOB,再根据角平分线的定义即可求出∠BOC,从而求出∠COE;
(2)先分别求出OC与OD重合时、OE与OD重合时和OC与OA重合时运动时间,再根据t的取值范围分类讨论,分别画出对应的图形,根据等量关系列出方程求出t即可;
(3)先分别求出OE与OB重合时、OC与OA重合时、OC为OA的反向延长线时运动时、OE为OB的反向延长线时运动时间,再根据m的取值范围分类讨论,分别画出对应的图形,根据等量关系列出方程求出m即可;
解:(1)∵![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,
∴∠BOD=90°,∠BOE=∠DOE=![]() ∠BOD =45°
∠BOD =45°
∵![]()
∴∠AOB=∠AOE+∠BOE=130°
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠AOC=∠BOC=![]() =65°
=65°
∴∠COE=∠BOC-∠BOE=20°
(2)由原图可知:∠COD=∠DOE-∠COE=25°,
故OC与OD重合时运动时间为25°÷5°=5s;OE与OD重合时运动时间为45°÷5°=9s;OC与OA重合时运动时间为65°÷5°=13s;
①当![]() 时,如下图所示
时,如下图所示
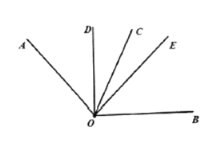
∵∠AOD=∠AOB-∠BOD=40°,∠COE=20°
∴∠AOD≠∠COE
∴∠AOD+∠COD≠∠COE+∠COD
∴此时![]() ;
;
②当![]() 时,如下图所示
时,如下图所示
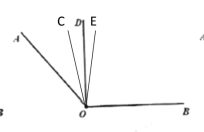
∵∠AOD=∠AOB-∠BOD=40°,∠COE=20°
∴∠AOD≠∠COE
∴∠AOD-∠COD≠∠COE-∠COD
∴此时![]() ;
;
③当![]() 时,如下图所示:
时,如下图所示:
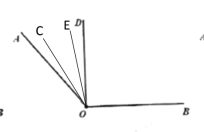
OC和OE旋转的角度均为5t
此时∠AOC=65°-5t,∠DOE=5t-45°
∵![]()
∴65-5t=5t-45
解得:t=11
综上所述:当![]() =11时,
=11时,![]() .
.
(3)OE与OB重合时运动时间为45°÷5°=9s;OC与OA重合时运动时间为65°÷10°=6.5s; OC为OA的反向延长线时运动时间为(180°+65°)÷10=24.5s;OE为OB的反向延长线时运动时间为(180°+45°)÷5=45s;
①当![]() ,如下图所示
,如下图所示
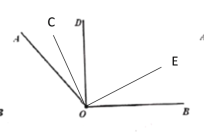
OC旋转的角度均为10m, OE旋转的角度均为5m
∴此时∠AOC=65°-10m,∠BOE=45°-5m
∵![]()
∴65-10m =![]() (45-5m)
(45-5m)
解得:m =![]() ;
;
②当![]() ,如下图所示
,如下图所示
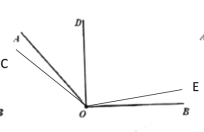
OC旋转的角度均为10m, OE旋转的角度均为5m
∴此时∠AOC=10m-65°,∠BOE=45°-5m
∵![]()
∴10m-65=![]() (45-5m)
(45-5m)
解得:m =![]() ;
;
③当![]() ,如下图所示
,如下图所示
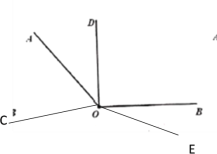
OC旋转的角度均为10m, OE旋转的角度均为5m
∴此时∠AOC=10m-65°,∠BOE=5m-45°
∵![]()
∴10m-65=![]() (5m-45)
(5m-45)
解得:m =![]() ,不符合前提条件,故舍去;
,不符合前提条件,故舍去;
综上所述:m=![]() 或
或![]() .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案