Question

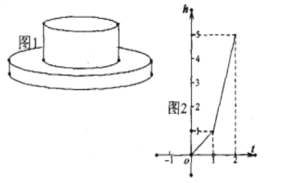
【题目】如图1是一个有两个圆柱形构成的容器，最下面的圆柱形底面半径。匀速地向空容器内注水，水面高度（单位：米）与时间（单位：小时）的关系如图2所示。

（1）求水面高度与时间的函数关系式；

（2）求注水的速度（单位：立方米/每小时），并求容器内水的体积与注水时间的函数关系式；

（3）求上面圆柱的底面半径（壁厚忽略不计）。

Answer 1

【答案】（1）；（2）；（3）4

【解析】

（1）由待定系数法可求水面高度h与时间t的函数关系式；

（2）由下面的圆柱形的体积=注水的速度×时间，可列方程，求出注水速度，即可求容器内水的体积V与注水时间t的函数关系式；

（3）由上面的圆柱形的体积=注水的速度×时间，可列方程，求解即可．

（1）当0≤t≤1时，设水面高度h与时间t的函数关系式：h=kt，且过（1，1）

∴1=k

∴当0≤t≤1时，设水面高度h与时间t的函数关系式：h=t

当1＜t≤2时，设水面高度h与时间t的函数关系式：h=mt+n，且过（1，1），（2，5）

∴

解得：

∴当1＜t≤2时，设水面高度h与时间t的函数关系式：h=4t-3

所以水面高度与时间的函数关系是

（2）由图2知，注满下面圆柱所花的时间是小时，下面圆柱的高度是米，设注水的速度为立方米/每小时，那么有

得注水的速度（立方米∕每小时）；

容器内水的体积与注水时间的函数关系式为：

（3）由题意知，上面圆柱的容积与下面圆柱的容积相等，且它的高度为4米，

于是有，解得

即上面圆柱的底面半径为米.