题目内容
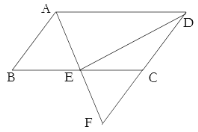
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接AD、DB、DF,求出∠AFD=∠ABD=90°,根据HL证两三角形全等得出∠FAD=60°,求出AD∥EF∥GI,过F作FZ⊥GI,过E作EN⊥GI于N,得出平行四边形FZNE得出EF=ZN=![]() a,求出GI的长,求出第一个正六边形的边长是
a,求出GI的长,求出第一个正六边形的边长是![]() a,是等边三角形QKM的边长的
a,是等边三角形QKM的边长的![]() ;同理第二个正六边形的边长是等边三角形GHI的边长的
;同理第二个正六边形的边长是等边三角形GHI的边长的![]() ;求出第五个等边三角形的边长,乘以
;求出第五个等边三角形的边长,乘以![]() 即可得出第六个正六边形的边长.
即可得出第六个正六边形的边长.
连接AD、DF、DB.
∵六边形ABCDEF是正六边形,
∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,
∴∠EFD=∠EDF=∠CBD=∠BDC=30°,
∵∠AFE=∠ABC=120°,
∴∠AFD=∠ABD=90°,
在Rt△ABD和RtAFD中
![]()
∴Rt△ABD≌Rt△AFD(HL),
∴∠BAD=∠FAD=![]() ×120°=60°,
×120°=60°,
∴∠FAD+∠AFE=60°+120°=180°,
∴AD∥EF,
∵G、I分别为AF、DE中点,
∴GI∥EF∥AD,
∴∠FGI=∠FAD=60°,
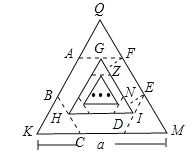
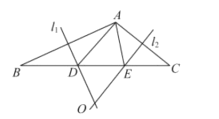
∵六边形ABCDEF是正六边形,△QKM是等边三角形,
∴∠EDM=60°=∠M,
∴ED=EM,
同理AF=QF,
即AF=QF=EF=EM,
∵等边三角形QKM的边长是a,
∴第一个正六边形ABCDEF的边长是![]() a,即等边三角形QKM的边长的
a,即等边三角形QKM的边长的![]() ,
,
过F作FZ⊥GI于Z,过E作EN⊥GI于N,
则FZ∥EN,
∵EF∥GI,
∴四边形FZNE是平行四边形,
∴EF=ZN=![]() a,
a,
∵GF=![]() AF=
AF=![]() ×
×![]() a=
a=![]() a,∠FGI=60°(已证),
a,∠FGI=60°(已证),
∴∠GFZ=30°,
∴GZ=![]() GF=
GF=![]() a,
a,
同理IN=![]() a,
a,
∴GI=![]() a+
a+![]() a+
a+![]() a=
a=![]() a,即第二个等边三角形的边长是
a,即第二个等边三角形的边长是![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是![]() ×
×![]() a;
a;
同理第第三个等边三角形的边长是![]() ×
×![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是![]() ×
×![]() ×
×![]() a;
a;
同理第四个等边三角形的边长是![]() ×
×![]() ×
×![]() a,第四个正六边形的边长是
a,第四个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第五个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a,第五个正六边形的边长是
a,第五个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第六个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,第六个正六边形的边长是
a,第六个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,
a,
即第六个正六边形的边长是![]() ×
×![]() a,
a,
故选A.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案【题目】一个运输公司有甲、乙两种货车,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运货吨数 | |
第一次 | 2 | 4 | 18 |
第二次 | 5 | 6 | 35 |
(1)求甲、乙两种货车每次满载分别能运输多少吨货物;
(2)现有一批重34吨的货物需要运输,而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输,为了使保养费用不超过700元,公司该如何安排甲、乙两种货车来完成这次运输任务.