题目内容
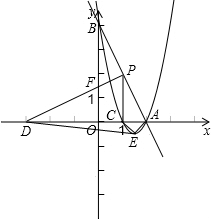
已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.
(1)求该抛物线的表达式;
(2)点D的坐标为(-3,0),点P为线段AB上的一点,当锐角∠PDO的正切值是
时,求点P的坐标;
(3)在(2)的条件下,该抛物线上的一点E在x轴下方,当△ADE的面积等与四边形APCE的面积时,求点E的坐标.

(1)求该抛物线的表达式;
(2)点D的坐标为(-3,0),点P为线段AB上的一点,当锐角∠PDO的正切值是
| 1 |
| 2 |
(3)在(2)的条件下,该抛物线上的一点E在x轴下方,当△ADE的面积等与四边形APCE的面积时,求点E的坐标.

(1)令y=0,则-2x+4=0,
解得x=2,
令x=0,则y=4,
所以,点A(2,0),B(0,4),
∵AC=1,且OC<OA,
∴点C的坐标为(1,0),
∵抛物线y=ax2+bx+c(a≠0)经过点A、B、C,
∴
,
解得
,
∴该抛物线的表达式为y=2x2-6x+4;
(2)∵D的坐标为(-3,0),
∴OD=3,
设PD与y轴的交点为F,
∵∠PDO的正切值是
,
∴OF=
•OD=
×3=
,
∴点F的坐标为(0,
),
设直线PD的解析式为y=kx+b(k≠0,k、b为常数),
则
,
解得
,
所以,直线PD的解析式为y=
x+
,
联立
,
解得
,
∴点P的坐标为(1,2);
(3)设点E到x轴的距离为h,
∵A(2,0),C(1,0),D(-3,0),
∴AC=1,AD=2-(-3)=5,
∵△ADE的面积等于四边形APCE的面积,
∴
×5h=
×1h+
×1×2,
解得h=
,
∵点E在x轴的下方,
∴点E的纵坐标为-
,
∴2x2-6x+4=-
,
整理得,4x2-12x+9=0,
解得x=
,
∴点E的坐标为(
,-
).
解得x=2,
令x=0,则y=4,
所以,点A(2,0),B(0,4),
∵AC=1,且OC<OA,
∴点C的坐标为(1,0),
∵抛物线y=ax2+bx+c(a≠0)经过点A、B、C,
∴
|
解得
|
∴该抛物线的表达式为y=2x2-6x+4;
(2)∵D的坐标为(-3,0),
∴OD=3,
设PD与y轴的交点为F,
∵∠PDO的正切值是
| 1 |
| 2 |
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴点F的坐标为(0,
| 3 |
| 2 |
设直线PD的解析式为y=kx+b(k≠0,k、b为常数),
则
|
解得
|
所以,直线PD的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
联立
|
解得
|
∴点P的坐标为(1,2);
(3)设点E到x轴的距离为h,
∵A(2,0),C(1,0),D(-3,0),
∴AC=1,AD=2-(-3)=5,
∵△ADE的面积等于四边形APCE的面积,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得h=
| 1 |
| 2 |
∵点E在x轴的下方,
∴点E的纵坐标为-
| 1 |
| 2 |
∴2x2-6x+4=-
| 1 |
| 2 |
整理得,4x2-12x+9=0,
解得x=
| 3 |
| 2 |
∴点E的坐标为(
| 3 |
| 2 |
| 1 |
| 2 |


练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目


 别与y轴交于O、A两点,与直线
别与y轴交于O、A两点,与直线