Question

将函数y=

3

3

x的图象向上平移2个单位，得到一个新函数，平移前后的两个函数图象分别与y轴交于O、A两点，与直线x=-

3

分别交于C、B两点．
（1）求这个新函数的解析式；
（2）判断以A、B、C、O四点为顶点的四边形形状，并说明理由；
（3）若（2）中的四边形（不包括边界）始终覆盖着二次函数y=x²-2bx+b²+

1

2

的图象的一部分，求满足条件的实数b的取值范围．

Answer 1

（1）y=

3

3

x+2．（2分）

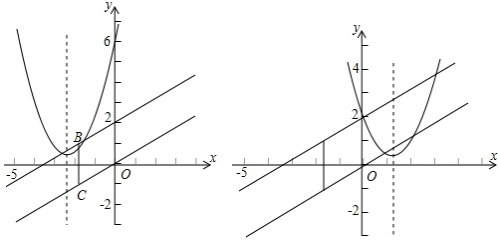
（2）答：四边形AOCB为菱形（3分）
由题意可得AB∥CO，BC∥AO，AO=2
∴四边形AOCB为平行四边形（4分）
易得A（0，2），B(-

3

，1)．
由勾股定理可得AB=2，
∴AB=AO（5分）
∴平行四边形AOCB为菱形（6分）

（3）二次函数y=x2-2bx+b2+

1

2

，
化为顶点式为：y=(x-b)2+

1

2

（7分）
∴抛物线顶点在直线y=

1

2

上移动
假设四边形的边界可以覆盖到二次函数，
则B点和A点分别是二次函数与四边形接触的边界点
将B(-

3

，1)，
代入二次函数，
解得b=-

3

-

2

2

，b=-

3

+

2

2

（不合题意，舍去）（8分）
将A（0，2），代入二次函数，
解得b=

6

2

，b=-

6

2

（不合题意，舍去）（9分）
所以实数b的取值范围：-

3

-

2

2

＜b＜

6

2

．（10分）