题目内容
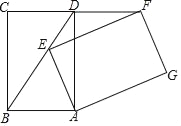
【题目】已知四边形ABCD是⊙O的内接四边形,∠DAB=120°,BC=CD,AD=4,AC=7,求AB的长度.
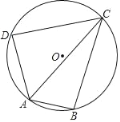
【答案】AB=3.
【解析】
作DE⊥AC,BF⊥AC,根据弦、弧、圆周角、圆心角的关系,求得![]() ,进而得到∠DAC=∠CAB=60°,在Rt△ADE中,根据60°锐角三角函数值,可求得DE=2
,进而得到∠DAC=∠CAB=60°,在Rt△ADE中,根据60°锐角三角函数值,可求得DE=2![]() ,AE=2,再由Rt△DEC中,根据勾股定理求出DC的长,在△BFC和△ABF中,利用60°角的锐角三角函数值及勾股定理求出AF的长,然后根据求出的两个结果,由AB=2AF,分类讨论求出AB的长即可.
,AE=2,再由Rt△DEC中,根据勾股定理求出DC的长,在△BFC和△ABF中,利用60°角的锐角三角函数值及勾股定理求出AF的长,然后根据求出的两个结果,由AB=2AF,分类讨论求出AB的长即可.
作DE⊥AC,BF⊥AC,
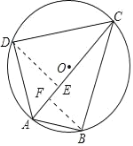
∵BC=CD,
∴![]() ,
,
∴∠CAB=∠DAC,
∵∠DAB=120°,
∴∠DAC=∠CAB=60°,
∵DE⊥AC,
∴∠DEA=∠DEC=90°,
∴sin60°=![]() ,cos60°=
,cos60°=![]() ,
,
∴DE=2![]() ,AE=2,
,AE=2,
∵AC=7,
∴CE=5,
∴DC=![]() ,
,
∴BC=![]() ,
,
∵BF⊥AC,
∴∠BFA=∠BFC=90°,
∴tan60°=![]() ,BF2+CF2=BC2,
,BF2+CF2=BC2,
∴BF=![]() AF,
AF,
∴![]() ,
,
∴AF=2或AF=![]() ,
,
∵cos60°=![]() ,
,
∴AB=2AF,
当AF=2时,AB=2AF=4,
∴AB=AD,
∵DC=BC,AC=AC,
∴△ADC≌△ABC(SSS),
∴∠ADC=∠ABC,
∵ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=∠ABC=90°,
但AC2=49,![]() ,
,
AC2≠AD2+DC2,
∴AB=4(不合题意,舍去),
当AF=![]() 时,AB=2AF=3,
时,AB=2AF=3,
∴AB=3.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目