题目内容
【题目】如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB，交BC于点D，DE⊥AB于点E，且AB＝6cm，则△DEB的周长为（ ）
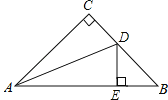
A.4cmB.6cmC.8cmD.以上都不对
【答案】B
【解析】
根据角平分线上的点到角的两边的距离相等可得CD＝DE，根据全等三角形对应边相等可得AC＝AE, 求出△DEB的周长＝AB．
解：∵AD平分∠CAB，∠C＝90°，DE⊥AB，
∴CD＝DE，
在△ACD和△AED中，
，
∴△ACD≌△AED（HL），
∴AC＝AE，
∴可得△DEB的周长＝BD+DE+BE，
＝BD+CD+BE，
＝BC+BE，
＝AC+BE，
＝AE+BE，
＝AB，
∵AB＝6cm，
∴△DEB的周长为6cm．
故选：B．
练习册系列答案
相关题目
【题目】甲、乙两名队员参加设计训练，成绩分别被制成下列两个统计图：
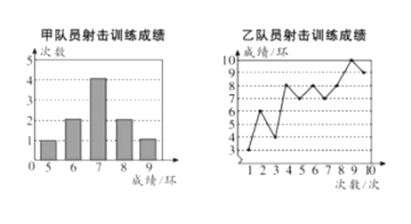
根据以上信息，整理分析数据如下：
平均数（环） | 中位数（环） | 众数（环） | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
（1）表格中
，
，
；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩，若选派其中一名参赛，你认为应选哪名队员？
（3）如果乙再射击
次，命中
环，那么乙的射击成绩的方差 ．（填“变大”“变小”或“不变”）
