题目内容
【题目】已知等边△ABC,D是BC上一点,E是平面上一点,且DE=AD,∠ADE=60°,连接CE.
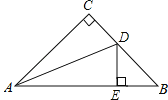
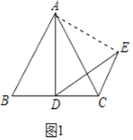
(1)当点D是线段BC的中点时,如图1.判断线段BD与CE的数量关系,并说明理由;
(2)当点D是线段BC上任意一点时,如图2.请找出线段AB,CE,CD三者之间的数量关系,并说明理由;
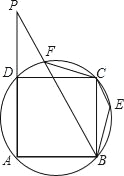
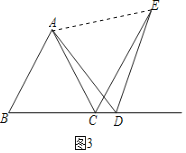
(3)当点D在线段BC的延长线上时,如图3,若△ABC边长为6,设CD=x,则线段CE= (用含x的代数式表示).

【答案】(1)BD=CE,理由见解析;(2)AB=CE+CD,理由见解析;(3)x+6.
【解析】
(1)连接AE,根据等边三角形的判定定理得到△ADE是等边三角形,根据等腰三角形的性质得到AD平分∠BAC,得到AC垂直平分DE,根据线段垂直平分线的定义证明结论;
(2)连接AE,证明△ABD≌△ACE,根据全等三角形的对应边相等解答;
(3)连接AE,证明△ABD≌△ACE,根据全等三角形的对应边相等得到BD=CE,代入计算得到答案.
(1)BD=CE,
证明:如图1,连接AE,
∵DE=AD,∠ADE=60°,
∴△ADE是等边三角形,
∴∠DAE=60°,
∵△ABC是等边三角形,D是BC的中点,
∴AD平分∠BAC,
∴∠DAC=30°,
∵∠DAE=60°,
∴AC平分∠DAE,
∵△ADE是等边三角形,
∴AC垂直平分DE,
∴CE=CD,
∵BD=CD,
∴CE=BD;
(2)AB=CE+CD,
证明:如图2,连接AE,
∵DE=AD,∠ADE=60°,
∴△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
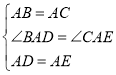
∴△ABD≌△ACE(SAS)
∴BD=CE,
∴AB=BC=BD+CD=CE+CD;
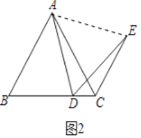
(3)如图3,连接AE,
∵DE=AD,∠ADE=60°,
∴△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
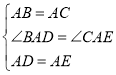 ,
,
∴△ABD≌△ACE(SAS)
∴BD=CE,
∴CE=BD=BC+CD=x+6,
故答案为:x+6.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图,试根据以上提供的信息解答下列问题:
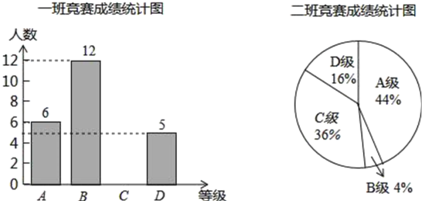
(1)把一班竞赛成绩统计图补充完整;
(2)根据下表填空:a= ,b= ,c= ;
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从平均数和中位数或众数中任选两个对这次竞赛成绩的结果进行分析.