题目内容
【题目】如图,函数 ![]() 的图像分别与 x轴、 y轴交于 A、 B两点,点 C在 y轴上, AC平分
的图像分别与 x轴、 y轴交于 A、 B两点,点 C在 y轴上, AC平分 ![]() .
.
(1) 求点 A、 B的坐标;
(2) 求 ![]() 的面积;
的面积;
(3) 点 P在坐标平面内,且以A、 B、P为顶点的三角形是等腰直角三角形,请你直接写出点 P的坐标.
【答案】(1)A(6,0),B(0,8);(2)15;(3)使△PAB为等腰直角三角形的P点坐标为(14,6)或(-2,-6)或(8,14)或(-8,2)或(-1,1)或(7,7).
【解析】
(1)在函数解析式中分别令y=0和x=0,解相应方程,可求得A、B的坐标;
(2)过C作CD⊥AB于点D,由勾股定理可求得AB,由角平分线的性质可得CO=CD,再根据S△AOB=S△AOC+S△ABC,可求得CO,则可求得△ABC的面积;
(3)可设P(x,y),则可分别表示出AP2、BP2,分∠PAB=90°、∠PBA=90°和∠APB=90°三种情况,分别可得到关于x、y的方程组,可求得P点坐标.
解:(1)在![]() 中,
中,
令y=0可得0=-![]() x+8,解得x=6,
x+8,解得x=6,
令x=0,解得y=8,
∴A(6,0),B(0,8);
(2)如图,过点C作CD⊥AB于点D,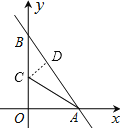
∵AC平分∠OAB,
∴CD=OC,
由(1)可知OA=6,OB=8,
∴AB=10,
∵S△AOB=S△AOC+S△ABC,
∴![]() ×6×8=
×6×8=![]() ×6×OC+
×6×OC+![]() ×10×OC,解得OC=3,
×10×OC,解得OC=3,
∴S△ABC=![]() ×10×3=15;
×10×3=15;
(3)设P(x,y),则AP2=(x-6)2+y2,BP2=x2+(y-8)2,且AB2=100,
∵△PAB为等腰直角三角形,
∴有∠PAB=90°、∠PBA=90°和∠APB=90°三种情况,
①当∠PAB=90°时,则有PA2=AB2且PA2+AB2=BP2,
即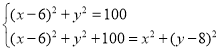 ,解得
,解得![]() 或
或![]() ,
,
此时P点坐标为(14,6)或(-2,-6);
②∠PBA=90°时,有PB2=AB2且PB2+AB2=PA2,
即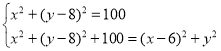 ,解得
,解得![]() 或
或![]() ,
,
此时P点坐标为(8,14)或(-8,2);
③∠APB=90°时,则有PA2=PB2且PA2+PB2=AB2,
即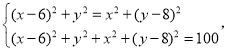 解得
解得![]() 或
或![]()
此时P点坐标为(-1,1)或(7,7);
综上可知使△PAB为等腰直角三角形的P点坐标为(14,6)或(-2,-6)或(8,14)或(-8,2)或(-1,1)或(7,7).

 阅读快车系列答案
阅读快车系列答案