题目内容
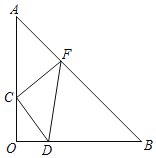
【题目】如图,△AOB中,∠AOB=90°,OA=OB,等腰直角△CDF的直角顶点C在边OA上,点D在边OB上,点F在边AB上,如果△CDF的面积是△AOB的面积的![]() ,OD=2,则△AOB的面积为____.
,OD=2,则△AOB的面积为____.
【答案】![]() .
.
【解析】
首先过点F作FM⊥AO,根据等腰直角三角形的性质判定△DOC≌△CMF,得出CM=OD=2,MF=OC,然后判定△AMF是等腰直角三角形,利用面积关系,构建一元二次方程,即可得解.
过点F作FM⊥AO于点M,如图:
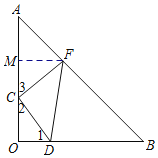
则有:∠O=∠FMC=90°,
∴∠1+∠2=90°,
∵等腰直角△CDF,
∴CF=CD,∠DCF=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠O=∠FMC=90°,CF=CD,
∴△DOC≌△CMF(AAS),
∴CM=OD=2,MF=OC,
∵∠AOB=90°,OA=OB,FM⊥AO,
∴△AMF是等腰直角三角形,
∴AM=MF=CO,
设AM=MF=CO=x,则OA=OB=2x+2,CD=CF=![]() ,
,
由△CDF的面积是△AOB的面积的![]() ,得:
,得:
![]() (
(![]() )2=
)2=![]() (2x+2)2,
(2x+2)2,
解得:x=1.5,
∴△AOB的面积=![]() (2x+2)2=
(2x+2)2=![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目