题目内容
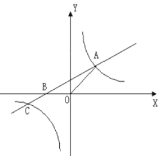
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 交于点
交于点![]() ,其中点
,其中点![]() 在第一象限,点
在第一象限,点![]() 在第三象限。
在第三象限。
(1)求双曲线的解析式;
(2)求![]() 点的坐标;
点的坐标;
(3)若![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,请写出
是等腰三角形?若存在,请写出![]() 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
【答案】(1)![]() ;(2)A(2,2);(3)存在.P(2,0).
;(2)A(2,2);(3)存在.P(2,0).
【解析】
(1)根据反比例函数的定义得到2m+1=﹣1,解方程得到m的值,即可确定双曲线的解析式;
(2)由y![]() x+1和双曲线的解析式组成方程组,解方程组即可得到A点的坐标;
x+1和双曲线的解析式组成方程组,解方程组即可得到A点的坐标;
(3)设P点坐标为(x,0),利用三角形的面积公式即可得到x的方程,解方程即可.
(1)根据题意得:2m+1=﹣1,解得:m=﹣1,
所以双曲线的解析式为y![]() ;
;
(2)联立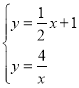 ,解得:
,解得:![]() 或
或![]() ,∴A点坐标为(2,2);
,∴A点坐标为(2,2);
(3)存在.理由如下:
设P点坐标为(x,0).
∵S△AOP=2,∴![]() 2|x|=2,∴x=±2,∴点P的坐标为(﹣2,0)或(2,0).
2|x|=2,∴x=±2,∴点P的坐标为(﹣2,0)或(2,0).
当P的坐标为(﹣2,0)时,△AOP不是等腰三角形,舍去;
当P的坐标为(2,0)时,OP=AP=2,△AOP是等腰三角形.
综上所述:P的坐标为(2,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目