题目内容
【题目】已知二次函数y＝﹣x2+2x+3．
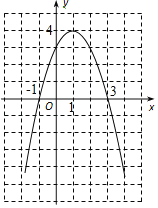
（1）在下面的直角坐标系中画出函数的图象；
（2）写出函数的3条性质．
【答案】（1）见解析；（2）①抛物线与x轴交与（﹣1，0）和（3，0），②与y轴交与点（0，3）③当y为正数时，﹣1＜x＜3④当﹣2＜x＜2时，﹣5＜y≤4；
【解析】
（1）配方后即可确定顶点坐标及对称轴，确定顶点坐标及对称轴、与坐标轴的交点坐标即可确定抛物线的解析式；（2）根据图象利用数形结合的方法确定答案即可．
解：（1）y＝﹣x2+2x+3＝﹣（x2﹣2x+1﹣4）＝﹣（x﹣1）2+4
对称轴为直线x＝1，顶点坐标为（1，4），如图所示．
（2）①抛物线与x轴交与（﹣1，0）和（3，0），
②与y轴交与点（0，3）
③当y为正数时，﹣1＜x＜3
④当﹣2＜x＜2时，﹣5＜y≤4；
练习册系列答案
阅读快车系列答案
相关题目
