Question

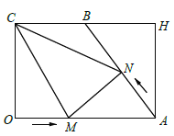
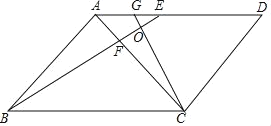
【题目】如图，ABCD中，∠BAC＝90°，AB＝AC，点E是边AD上一点，且BE＝BC，BE交AC于点F，过点C作BE的垂线，垂足为点O，与AD交于点G.

(1)若AB＝，求AE的长；

(2)求证；BF＝CO+EO.

Answer 1

【答案】(1)AE=﹣1；(2)证明见解析.

【解析】

(1)过E作EH⊥BA交BA的延长线于于H，根据等腰直角三角形的性质得到∠ABC＝45°，BC＝BE＝2，根据平行线的性质得到∠HAE＝∠ABC＝45°，设AH＝HE＝a，得到AE＝a，根据勾股定理即可得到结论；

(2)由(1)知，∠OBC＝30°，得到BF＝OB﹣OF＝OC﹣OE，过G作GH⊥BC于H，求出OE＝(2﹣)OC，把OE＝(2﹣)OC代入OC﹣OE求得BF＝2(﹣1)OC，代入求得CO+EO＝2(﹣1)OC，于是得到结论.

解：(1)过E作EH⊥BA交BA的延长线于于H，

∵∠BAC＝90°，AB＝AC，

∴∠ABC＝45°，BC＝BE＝2，

∵AD∥BC，

∴∠HAE＝∠ABC＝45°，

∴设AH＝HE＝a，

∴AE＝a，

在Rt△EBH中，∵BH2+EH2＝BE2，

∴(a+)2+a2＝22，

∴a＝，

∴AE＝﹣1；

(2)过A作AM⊥BC于M，GH⊥BC于H，EN⊥BC于N，

则AM＝GH＝EN＝BC＝1，

∴sin∠EBC＝，

∴∠EBC＝30°，

∴OC＝BC＝1，

∴∠OBC＝30°，

∵BE＝BC，

∴∠BEC＝75°，

∵∠CFE＝45°+30°＝75°，

∴CF＝CE，

∴OF＝OE，

∵OC⊥BO，

∴BO＝OC，

∴BF＝OB﹣OF＝OC﹣OE，

过G作GH⊥BC于H，

∴GH＝EN＝OC＝CG＝(OC+OG)＝(OC+OE)，

∴OC＝(OC+OE)，

∴OE＝(2﹣)OC，

∴BF＝OB﹣OF＝OC﹣OE＝2(﹣1)OC，

∵CO+EO＝OC+(2﹣)OC＝2(﹣1)OC，

∴BF＝CO+EO.