题目内容
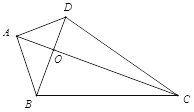
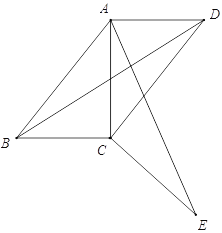
【题目】如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
(1)求证:AE⊥BD;
(2)若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由题意可得△ABC是等腰直角三角形,由旋转得![]() ,再由对顶角相等,三角形内角和可得
,再由对顶角相等,三角形内角和可得![]() ,即
,即 ![]() ;
;
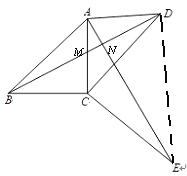
(2)如图,连接![]() ,依次证出△DCE是等腰直角三角形、△ADE是直角三角形,运用勾股定理得DE、AE的长,又因为BD=AE,从而求解.
,依次证出△DCE是等腰直角三角形、△ADE是直角三角形,运用勾股定理得DE、AE的长,又因为BD=AE,从而求解.
(1)证:由题意可得 ![]() ,
,![]() ,∴
,∴![]() .
.
设 ![]() 与
与 ![]() 、
、![]() 分别交于点
分别交于点 ![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,即
,即 ![]() .
.
(2)解:连接![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目