题目内容
【题目】为了保障人畜饮水安全,某县急需饮水设备12台,现有甲、乙两种设备可供选择,已知购买1台甲种设备和2台乙两种设备共需10000元,购买3台甲种设备和1台乙两种设备共需15000元,且甲种设备的安装及运输费用为600元/台,乙种设备的安装及运输费用为800元/台.
(1)购买1台甲、乙两种设备各需多少元?
(2)若购买的费用不超过40000元,安装及运输费用不超过9200元,则有几种购买方案?
【答案】(1)购买1台甲设备需4000元,购买1台乙设备需3000元;(2) 可购买甲种设备2台、乙种设备10台;或甲种设备3台、乙种设备9台;甲种设备4台、乙种设备8台.
【解析】
(1)根据“购买1台甲种设备和2台乙两种设备共需10000元”,“购买3台甲种设备和1台乙两种设备共需15000元”作为等量关系列方程组,解方程组即可求解;
(2)根据“购买的费用不超过40000元”,“安装及运输费用不超过9200元”作为不等关系列不等式组,求其整数解即可求解.
(1)设购买1台甲设备各需m元,购买1台乙设备各需n元,依题意有
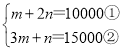 ,
,
解得
![]() .
.
答:购买1台甲设备各需4000元,购买1台乙设备各需3000元.
(2)设购买甲种设备x台,则购买乙种设备(12-x)台,
购买设备的费用为:4000x+3000(12-x)≤40000,
安装及运费用为:600x+800(12-x),
根据题意得
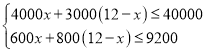 ,
,
解得2≤x≤4,
∵x是整数,
∴有3种方案,即x=2,3,4,
①购买甲种设备2台,乙种设备10台;
②购买甲种设备3台,乙种设备9台;
③购买甲种设备4台,乙种设备8台.
答:可购买甲种设备2台、乙种设备10台,或甲种设备3台、乙种设备9台,甲种设备4台、乙种设备8台.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目