Question

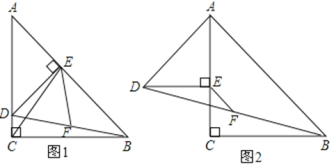
【题目】在△ABC和△ADE中AC=BC,AE=DE , ∠ACB=∠AED=90° , 点E在AB上,F是线段BD的中点,连接CE、FE.

（1）若AD=3,BE=4 ,求EF的长

（2）求证：CE=EF

（3）将图1中的△ADE绕点A顺时针旋转,使△AED的一边AE恰好与△ABC的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.

Answer 1

【答案】（1）2.5；（2）见解析；（3）成立，见解析

【解析】

（1）根据等腰直角三角形的性质求得DE长，再根据勾股定理求得BD长，由直角三角形斜边中线等于斜边一半可求；

（2）通过角之间的关系证出，判断出△ECF是等腰直角三角形，斜边和直角边的关系即为结论；

（3）连接CF,延长EF交CB于点G,通过辅助线构建全等模型，即，通过全等三角形的性质证明；也可证明，利用全等三角形的对应边相等，再结合垂直平分线的性质证明.

解:（1） ，,

,

在中,

又是线段BD的中点, EF=BD=2.5;

（2）如图1,连接CF,线段CE与FE之间的数量关系是

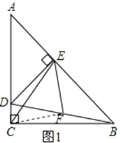
、C、D、E四点共圆

且BD是该圆的直径,

点F是BD的中点,

点F是圆心,,

:

,

∴△ECF是等腰直角三角形，

.

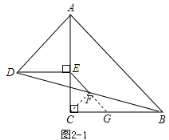
（3）（1）中的结论仍然成立.

解法1:如图,连接CF,延长EF交CB于点G,

,

,

在和中,

,

,

,

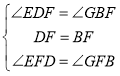为等腰直角三角形,

,

；

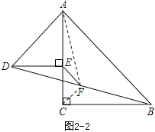
解法2:如图,连结CF、AF,

,

点F是BD的中点,

,

在和中,

,

,

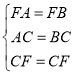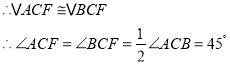∵FA=FB,CA=CB,

∴CF所在的直线垂直平分线段AB，

同理,EF所在的直线垂直平分线段AD,

∵DA⊥BA,

∴EF⊥CF,

为等腰直角三角形

.