题目内容
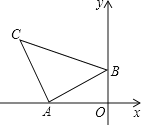
【题目】如图,△ABC是等腰直角三角形,∠BAC=90°,其中A(-2,0),B(0,1),则直线BC的函数表达式为______.
【答案】y=-![]() x+1
x+1
【解析】
先确定出OA=2,OB=1,再证明△AOB≌△CDA,得出AD=1,CD=2,求出C点坐标,然后利用待定系数法求出直线BC的函数表达式.
解:如图,∵A(-2,0),B(0,1),
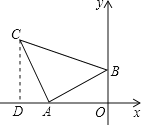
∴OA=2,OB=1.
过点C作CD⊥x轴于D,
∴∠CAD+∠ACD=90°,
∵∠BAC=90°,
∴∠CAD+∠OAB=90°,
∴∠OAB=∠ACD.
在△AOB和△CDA中,
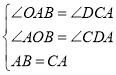 ,
,
∴△AOB≌△CDA,
∴AD=BO=1,CD=AO=2,
∴OD=OA+AD=3,
∴C(-3,2).
设直线BC的函数表达式为y=kx+b,
∵B(0,1),C(-3,2),
∴![]() ,
,
解得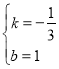 ,
,
∴直线BC的函数表达式为y=![]() x+1.
x+1.
故答案为y=![]() x+1.
x+1.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目