题目内容
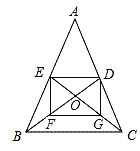
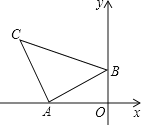
【题目】如图,□ABCD中,对角线AC与AB、AD的夹角分别为α、β,点E是AC上任意一点,给出如下结论:①AB sinα=AD sinβ;②S△ABE=S△ADE;③ADsinα=AB sinβ. 其中正确的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
【答案】C
【解析】分析:
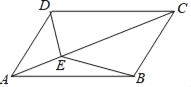
如下图,(1)过点D作DN⊥AC于点N,过点B作BM⊥AC于点M,由此可得DN=AD·sinβ,BM=AB·sinα,由已知条件易证△ABC≌△CDA,从而可得S△ABC=![]() ACAB·sinα=
ACAB·sinα=![]() ACAD·sinβ,由此可得AB· sinα=AD· sinβ,即结论①成立;(2)由S△ABE=
ACAD·sinβ,由此可得AB· sinα=AD· sinβ,即结论①成立;(2)由S△ABE=![]() AEABsinα,S△ADE=
AEABsinα,S△ADE=![]() AEAdsinβ结合(1)中所得AB·sinα=AD·sinβ即可得到S△ABE=S△ADE,故结论②成立;(3)由已知条件易证△ADN≌△CBM,由此可得DN=BM,即AD·sinβ=AB·sinα,AD·sinα=AB·
AEAdsinβ结合(1)中所得AB·sinα=AD·sinβ即可得到S△ABE=S△ADE,故结论②成立;(3)由已知条件易证△ADN≌△CBM,由此可得DN=BM,即AD·sinβ=AB·sinα,AD·sinα=AB·![]() ,由此可知只有当
,由此可知只有当![]() =
=![]() 时,才有ADsinα=ABsinβ成立,故结论③不一定成立;
时,才有ADsinα=ABsinβ成立,故结论③不一定成立;
详解:
由题意,可知∠CAB=α,∠DAC=β,如下图,过点D作DN⊥AC于点N,过点B作BM⊥AC于点M,
∴DN=AD·sinβ,BM=AB·sinα,
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
在△ABC与△CDA中,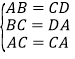 ,
,
∴△ABC≌△CDA,
∴S△ABC=S△CDA,
∵S△ABC=![]() ACABsinα,S△CDA=
ACABsinα,S△CDA=![]() ACADsinβ,
ACADsinβ,
∴AB·sinα=AD·sinβ,①正确;
(2)∵S△ABE=![]() AEABsinα,S△ADE=
AEABsinα,S△ADE=![]() AEADsinβ,且AB·sinα=AD·sinβ,
AEADsinβ,且AB·sinα=AD·sinβ,
∴S△ABE=S△ADE,②正确;
(3)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAN=∠BCM,
又∵∠DNA=∠BMC=90°,
∴△ADN≌△CBM,
∴DN=BM,
∴AD·sinβ=AB·sinα,
∴AD·sinα=AB·![]() ,
,
由此可知只有当![]() =
=![]() 时,才有ADsinα=AB sinβ成立,故结论③不一定成立;
时,才有ADsinα=AB sinβ成立,故结论③不一定成立;
综上所述,3个结论中,只有①②成立.
故选C.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
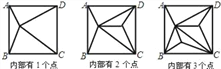
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2008个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.