Question

【题目】5月23、24日，兰州市九年级学生进行了中考体育测试，某校抽取了部分学生的一分钟跳绳测试成绩，将测试成绩整理后作出如统计图．甲同学计算出前两组的频率和是0．12，乙同学计算出第一组的频率为0.04，丙同学计算出从左至右第二、三、四组的频数比为4：17：15．结合统计图回答下列问题：

(1)这次共抽取了多少名学生的一分钟跳绳测试成绩？

(2)若跳绳次数不少于130次为优秀，则这次测试成绩的优秀率是多少？

(3)如果这次测试成绩中的中位数是120次，那么这次测试中，成绩为120次的学生至少有多少人？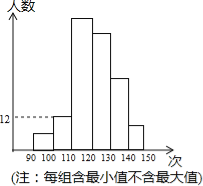

Answer 1

【答案】（1）150名（2） (3) 7人

【解析】解：（1）第二组的频率为0.12－0.04＝0.08，

又第二组的人数为12人，故总人数为： (人)。

∴这次共抽取了150名学生的一分钟跳绳测试成绩。

（2）第一组人数为150×0.04＝6(人)，第二组的人数为12人，

由第二、三、四组的频数比为4：17：15，设三组频数为4k，17 k，15 k，

由4k =12得k=3，∴第三组人数为51人，第四组人数为45人。

∴这次测试的优秀率为。

（3）前三组的人数为69，而中位数是第75和第76个数的平均数，所以成绩为120次的学生至少有7人。

（1）根据题意：结合各小组频数之和等于数据总和，各小组频率之和等于1；易得第二组的频率0.08；再由频数、频率和总量的关系可得总人数。

（2）根据题意：从左至右第二、三、四组的频数比为4：17：15，和(1)的结论；容易求得各组的人数，这样就能求出优秀率。

（3）由中位数的意义，作答即可。