题目内容
【题目】如图,△ABC中,点D在BC上,BC平分∠ABE,BE∥AC,∠ADB=60°,∠CAD=2∠BDE,AB=14,BD=16,BE=4,则CD=_____.

【答案】6.
【解析】
作AF⊥BC于BC相交于F,设FD=x,分别表示AF和BF,在Rt△ABF中根据勾股定理可解得x即FD的值(有两个),由此可求出DC,作∠DAC的平分线交DC于H,可证△EBD∽△HCA,根据相似三角形的性质可求得HC=3.5,由此可排除DC=10,所以可得DC=6.
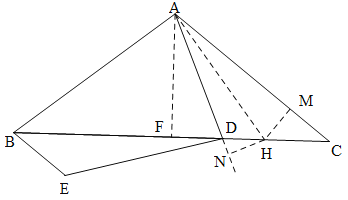
如图:作AF⊥BC于BC相交于F,作∠DAC的平分线交DC于H,过H分别作HN⊥AN,HM⊥AC,与AN的延长线和AC分别相交于N,M.
∵BC平分∠ABE,
∴∠ABC=∠EBC,
∵BE∥AC,
∴∠ACB=∠EBC,
∴∠ABC=∠ACB,
∴AB=AC=14,
∵AF⊥BC,
∴BF=FC,
设FD=x,
∵∠ADF=60°,BD=16,
∴AD=2x,AF![]() ,BF=16-x,DC=FC-DF=16-2x,
,BF=16-x,DC=FC-DF=16-2x,
在Rt△ABF中根据勾股定理![]() ,
,
即![]() ,解得x=3或x=5,
,解得x=3或x=5,
∴DC=10或DC=6,
∵∠DAC的平分线交DC于H,∠CAD=2∠BDE,
∴∠HAC=∠BDE,
又∵∠ABC=∠EBC,
∴△EBD∽△HCA,
∴![]() ,即
,即 ![]() ,解得HC=3.5,
,解得HC=3.5,
∵∠ADF=60°,
∴∠ADC=120°,
∴AC>AD,
∵HN⊥AN,HM⊥AC,∠DAC的平分线交DC于H,
∴HN=HM,
∴![]() ,
,
∴DH<HC,
∴DC=DH+HC<2HC<7,
故DC=6.
答案为:6.

练习册系列答案
相关题目








