题目内容
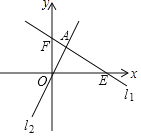
【题目】如图1,△ABC中,AB=AC,∠BEF=∠DBC,∠BDC=2∠DEF,

(1)求证:BD=BE;
(2)如图2,在(1)的下,EF⊥BC,BE=8,DG=5,求CD的长;
(3)在(2)的条件下,如图3,过点C作CM⊥CB交BD的延长线于M,过点B作∠NBC=∠MBC,连接MN,且△BMN的面形为45,求BN的长.
【答案】(1)证明见解析;(2)CD=3;(3)BN=15,
【解析】
(1)证明∠BDE=∠BED,根据等角对等边得出结论;
(2)作两条垂线段,证明△BEF≌△NBD和△BGF≌△DNC,进而判断出△BFG≌△DHC即可得出CD=3,
(3)先用射影定理求出DM=![]() =
=![]() ,BM=BD+DM=
,BM=BD+DM=![]() ,CM=
,CM=![]() =
=![]() ,进而得出BH=BM=
,进而得出BH=BM=![]() ,MH=2CM=
,MH=2CM=![]() ,再用S△BMN=S△BMH+S△MNH得出NI,进而用△BCH∽△NIH,得出
,再用S△BMN=S△BMH+S△MNH得出NI,进而用△BCH∽△NIH,得出![]() ,即求出NH=
,即求出NH=![]() ,即可得出结论.
,即可得出结论.
解:(1)∵AB=AC,
∴∠C=∠ABC,
∵∠BEF=∠DBC,
∴∠EFB=∠BDC,
设∠DEF=x,∠EDB=y,∠BEF=z,
在△EGD和△BGF中,x+y=z+2x,即y=x+z,即∠BDE=∠BED,
∴BD=BE,
(2)如图2,过D作DH⊥BC,
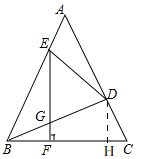
∵EF⊥BC,
∴∠BFE=∠DHB=90°
由(1)知:BE=BD,
∵∠BEF=∠DBC,∠EFB=∠DHB=90°,
∴△BEF≌△BDH(AAS),
∴BF=DH,∠EBF=∠BDH,
∵∠ABC=∠ACB,∠BEF+∠ABC=90°,.
∴∠BEF+∠ACB=90°,
∵∠BEF=∠DBC,
∴∠DBC+∠ACB=90°
∴∠BDC=90°,
∴∠BDH+∠CDH=90°,
∴∠FBG=∠HDC,
∵∠BFG=∠DHC,BF=DH,
∴△BFG≌△DHC(ASA),
∴CD=BG=BD﹣DG=3;
(3)如图3,由(2)知,CD=3,∠BDC=90°,
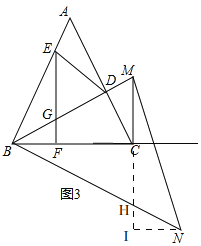
∴BC=![]() ,
,
在Rt△BCM中,CD⊥BM,
∴DM=![]() =
=![]() ,
,
∴BM=BD+DM=![]() ,CM=
,CM=![]() =
=![]() ,
,
延长MC交BN于H,
∵∠NBC=∠MBC,BC⊥MH,
∴BH=BM=![]() ,MH=2CM=
,MH=2CM=![]() ,
,
过点N作NI⊥MH交MH延长线于I,
∵△BMN的面形为45
![]() ∴NI=
∴NI=![]() ,
,
∵△BCH∽△NIH,
∴![]() ,
,
∴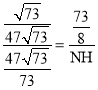 ,
,
∴NH=![]() ,
,
∴BN=BH+NH=![]() =15,
=15,

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案