题目内容
【题目】已知：如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作平行四边形ABDE，连接AD，EC．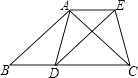 
（1）求证：AD=CE；
（2）当点D在什么位置时，四边形ADCE是矩形，请说明理由．
【答案】
（1）证明：∵AB=AC，
∴∠B=∠ACB，
又∵ABDE中，AB=DE，AB∥DE，
∴∠B=∠EDC=∠ACB，AC=DE，
在△ADC和△ECD中， 
，
∴△ADC≌△ECD（SAS）
（2）解：点D在BC的中点上时，四边形ADCE是矩形，理由如下：
∵四边形ABDE是平行四边形，
∴AE=BD，AE∥BC，
∵D为边长BC的中点，
∴BD=CD，
∴AE=CD，AE∥CD，
∴四边形ADCE是平行四边形，
∵△ADC≌△ECD，
∴AC=DE，
∴四边形ADCE是矩形
【解析】（1）利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB，则易证△ADC≌△ECD，利用全等三角形的对应边相等即可证得；（2）根据平行四边形性质推出AE=BD=CD，AE∥CD，得出平行四边形，根据AC=DE推出即可．
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动，组织150名学生参观历史博物馆和民俗展览馆，每一名学生只能参加其中一项活动，共支付票款2000元，票价信息如下：
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
（1）请问参观历史博物馆和民俗展览馆的人数各是多少人？
（2）若学生都去参观历史博物馆，则能节省票款多少元？
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整)，已知A.B两组捐款人数的比为1:5.
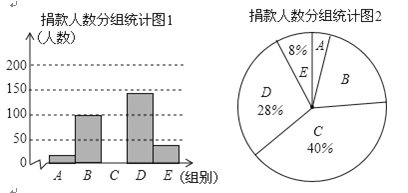
被调查的捐款人数分组统计表：
组别 | 捐款额x/元 | 人数 |
A | 1≤x＜10 | a |
B | 10≤x＜20 | 100 |
C | 20≤x＜30 | ______ |
D | 30≤x＜40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题：
(1)求a的值和参与调查的总人数；
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数；
(3)已知该校有学生2200人，请估计捐款数不少于30元的学生人数有多少人?
