Question

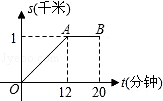
【题目】如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M是抛物线y= +bx+c的顶点，则抛物线y= +bx+c与直线y=1交点的个数是（ ）
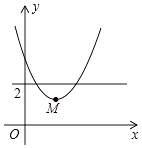
A.0个或1个
B.0个或2个
C.1个或2个
D.0个、1个或2个

Answer 1

【答案】D
【解析】解：由抛物线y=x2+bx+c的图象可知，该抛物线与x轴没有交点， 即：△＜0，
则：b2﹣4c＜0，
又点M是直线y=2与x轴之间的一个动点，点M的坐标为：（﹣ ， ），
所以，0＜ ＜2，即：﹣8＜b2﹣4c＜0，
令y=x2+bx+c﹣1，则要求方程x2+bx+c=1的解得个数，只需判定抛物线y=x2+bx+c﹣1与x轴有无交点及交点的个数即可．
又因为，△=b2﹣4ac=b2﹣4（c﹣1）=b2﹣4c+4，
所以，﹣4＜b2﹣4c+4＜4，
即：①当﹣4＜b2﹣4c+4＜0时，抛物线y=x2+bx+c﹣1与x轴没有交点；②b2﹣4c+4=0时，抛物线y=x2+bx+c﹣1与x轴有一个交点；③0＜b2﹣4c+4＜4时，抛物线y=x2+bx+c﹣1与x轴有两个交点．
故选：D．
【考点精析】根据题目的已知条件，利用二次函数的性质的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．