题目内容
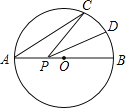
【题目】如图,AB是半径为1的⊙O的直径,点C在⊙O上,∠CAB=30°,D为劣弧CB的中点,点P是直径AB上一个动点,则PC+PD的最小值为( )
A.1B.2C.![]() D.
D.![]()
【答案】C
【解析】
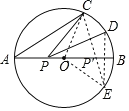
作D点关于AB的对称点E,连接OC.OE、CE,CE交AB于P',如图,利用对称的性质得到P'E=P'D,![]() ,再根据两点之间线段最短判断点P点在P'时,PC+PD的值最小,接着根据圆周角定理得到∠BOC=60°,∠BOE=30°,然后通过证明△COE为等腰直角三角形得到CE的长即可.
,再根据两点之间线段最短判断点P点在P'时,PC+PD的值最小,接着根据圆周角定理得到∠BOC=60°,∠BOE=30°,然后通过证明△COE为等腰直角三角形得到CE的长即可.
作D点关于AB的对称点E,连接OC、OE、CE,CE交AB于P',如图,
∵点D与点E关于AB对称,
∴P'E=P'D,![]() ,
,
∴P'C+P'D=P'C+P'E=CE,
∴点P点在P'时,PC+PD的值最小,最小值为CE的长度.
∵∠BOC=2∠CAB=2×30°=60°,
而D为![]() 的中点,
的中点,
∴∠BOE![]() ∠BOC=30°,
∠BOC=30°,
∴∠COE=60°+30°=90°,
∴△COE为等腰直角三角形,
∴CE![]() OC
OC![]() ,
,
∴PC+PD的最小值为![]() .
.
故选:C.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】某宾馆有若干间标准房,当标准房的价格为![]() 元时,每天入住的国间数为
元时,每天入住的国间数为![]() 间,经市场调查表明,该宾馆每间标准房的价格在
间,经市场调查表明,该宾馆每间标准房的价格在![]() 元之间(含
元之间(含![]() 元,
元,![]() 元)浮动时,每天人住的房间数
元)浮动时,每天人住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| …… | 190 | 200 | 210 | 220 | …… |
| …… | 65 | 60 | 55 | 50 | …… |
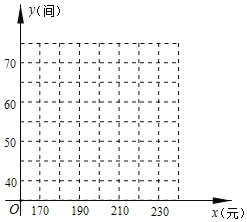
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)猜想(1)中的图象是什么函数的图象,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?