题目内容
【题目】已知,在直角坐标系中,平行四边形OABC的顶点A,C坐标分别为A(2,0),C(-1,2),反比例函数![]() 的图象经过点B (m≠0)
的图象经过点B (m≠0)
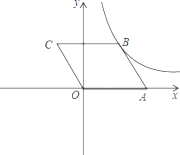
(1)求出反比例函数的解析式
(2)将![]() OABC沿着x轴翻折,点C落在点D处,做出点D并判断点D是否在反比例函数
OABC沿着x轴翻折,点C落在点D处,做出点D并判断点D是否在反比例函数![]() 的图象上
的图象上
(3)在x轴是否存在一点P使△OCP为等腰三角形,若存在,写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ; (2)在反比例函数图象上,理由见解析;(3)存在,点P的坐标(-
; (2)在反比例函数图象上,理由见解析;(3)存在,点P的坐标(-![]() ,0)、(
,0)、(![]() ,0)、(-2,0)和(-2.5,0)
,0)、(-2,0)和(-2.5,0)
【解析】
(1)根据平行四边形的性质可得AO=BC,再根据A、C点坐标可以算出B点坐标,再把B点坐标代入反比例函数解析式中即可求出m的值;
(2)根据翻折的性质得到点D(-1,-2),再将点D代入反比例函数解析式中进行判断;
(3)根据题意作出图形,写出坐标即可.
(1)设BC于y轴相交于点E,如图所示:

∵四边形OABC是平行四边形,
∴BC=AO,
∵A(2,0),
∴OA=2,
∴BC=2,
∵C(-1,2),
∴CE=1,
∴BE=BC-CE=2-1=1,
∴B(1,2),
∵反比例函数y=![]() 的图象经过点B,
的图象经过点B,
∴m=1×2=2,
∴反比例函数的解析式为:y=![]() ;
;
(2)∵将![]() OABC沿着x轴翻折,点C落在点D处,
OABC沿着x轴翻折,点C落在点D处,
∴D(-1,-2),
∵m=2,
∴反比例函数y=![]() ,
,
把D点坐标(-1,-2)代入函数解析式y=![]() 中得:左右两边相等,
中得:左右两边相等,
∴点D在反比例函数![]() 的图象上;
的图象上;
(3)以OC=![]() 为半径,点O为圆心,画圆交x轴于点P1(-
为半径,点O为圆心,画圆交x轴于点P1(-![]() ,0)和P2(
,0)和P2(![]() ,0);
,0);
以OC=![]() 为半径,点C为圆心,画圆交x轴于点P3(-2,0);
为半径,点C为圆心,画圆交x轴于点P3(-2,0);
作线段OC的垂直平分线,交x轴于点P4(-2.5,0).
所以存在,点P的坐标(-![]() ,0)、(
,0)、(![]() ,0)、(-2,0)和(-2.5,0).
,0)、(-2,0)和(-2.5,0).

 阶梯计算系列答案
阶梯计算系列答案【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制成如下统计图表(单位:cm):
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
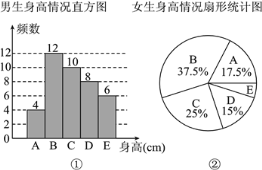
根据图表提供的信息,样本中,身高在160≤x<170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16