题目内容
【题目】如图,直线y=![]() x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=
x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=![]() 的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
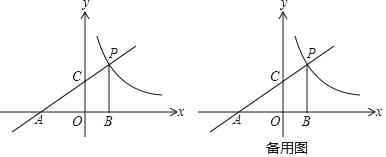
(1)直接写出点A的坐标_____;点C的坐标_____;点P的坐标_____;
(2)已知点Q在反比例函数y=![]() 的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
(3)设点R在反比例函数y=![]() 的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
【答案】 (﹣4,0) (0,2) (2,3)(2) M(5,0)(3) (1+![]() ,
,![]() )或(3,2)
)或(3,2)
【解析】试题分析:(1)利用待定系数法可以求出点A、C的坐标,由△ACO∽△APB,推出 ![]() ,推出OB=2,PB=3,由此即可解决问题.
,推出OB=2,PB=3,由此即可解决问题.
(2)如图1中,作点P关于x轴的对称点P′,连接QP′与x轴交于点M,LJ PM,此时PM+MQ的值最小.求出直线P′Q的解析式即可.
(3)设R点的坐标为(m, ![]() ),分两种情形分别利用相似三角形的性质,列出方程解决问题.
),分两种情形分别利用相似三角形的性质,列出方程解决问题.
试题解析:
(1)∵直线y=![]() x+2分别交x、y轴于点A、C,
x+2分别交x、y轴于点A、C,
∴A点坐标(﹣4,0),C点坐标(0,2),
∵S△AOC=![]() ×4×2=4,
×4×2=4,
∵OC∥PB,S△ABP=9,
∴△ACO∽△APB,
∴![]() ,
,
∴AB=6,PB=3,
∴OB=2,
∴P(2,3)
故答案为(﹣4,0),(0,2),(2,3).
(2)如图1中,作点P关于x轴的对称点P′,连接QP′与x轴交于点M,LJ PM,此时PM+MQ的值最小.
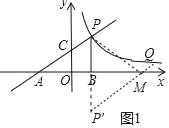
∵点P(2,3)在,反比例函数y=![]() 上,
上,
∴k=6,
∴Q(6,1),P′(2,﹣3),
∴直线P′Q是解析式为y=x﹣5,
令y=0,得x=5,
∴M(5,0).
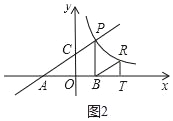
(3)如图2中,设R点的坐标为(m, ![]() ),
),
∵P点坐标为(2,3),
又∵△BRT∽△ACO,
∴![]() ,
,
∴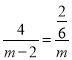 ,
,
解得m1=1+![]() ,m2=1﹣
,m2=1﹣![]() (舍去),
(舍去),
∴R(1+![]() ,
, ![]() ),
),
②如图3中,△BRT∽△CAO时,
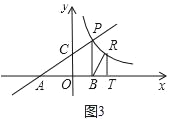
∴![]() 时,
时,
∴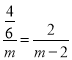 ,
,
解得m1=3,m2=﹣1(舍去)
∴R(3,2)
综上所述,满足条件的点R坐标为(1+![]() ,
, ![]() )或(3,2).
)或(3,2).