题目内容
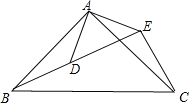
【题目】如图所示,△ABC中,D为AB的中点,DC⊥AC,且∠BCD=30°,求∠CDA的正弦值、余弦值和正切值.

【答案】![]() ,
,![]() ;
;![]() .
.
【解析】
过D作DE∥AC,交BC于点E,根据已知条件易证AC=2DE,由两直线平行内错角相等及垂直定义得到DC⊥DE,在RtCDE中,可得CE=2DE,DC=![]() DE.设DE=k,则CD=
DE.设DE=k,则CD=![]() ,AC=2k.在Rt△ACD中,利用勾股定理求得
,AC=2k.在Rt△ACD中,利用勾股定理求得![]() ,再根据锐角三角函数定义即可求出∠CDA的正弦值、余弦值和正切值.
,再根据锐角三角函数定义即可求出∠CDA的正弦值、余弦值和正切值.
过D作DE∥AC,交BC于点E,
∵AD=BD,
∴CE=EB,
即DE为△ABC的中位线,
∴AC=2DE,
又∵ DC⊥ AC,DE∥AC,
∴ DC⊥DE,即∠CDE=90°.
又∵ ∠BCD=30°,∴ EC=2DE,DC=![]() DE.
DE.
设DE=k,则CD=![]() ,AC=2k.
,AC=2k.
在Rt△ACD中,![]() .
.
∴ ![]() ,
,
![]() .
.
![]() .
.

练习册系列答案
相关题目