题目内容
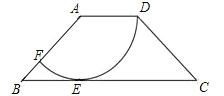
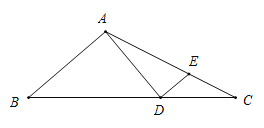
【题目】如图,在![]() ABC中,点D为BC边上的一点,且AD=AB=5, AD⊥AB于点A,过点D作DE⊥AD,DE交AC于点E,若DE=2,则
ABC中,点D为BC边上的一点,且AD=AB=5, AD⊥AB于点A,过点D作DE⊥AD,DE交AC于点E,若DE=2,则![]() ADC的面积为( )
ADC的面积为( )
A.![]() B.4C.
B.4C.![]() D.
D.![]()
【答案】D
【解析】
根据题意得出AB∥DE,得△CED∽△CAB,利用对应边成比例求CD长度,再根据等腰直角三角形求出底边上的高,利用面积公式计算即可.
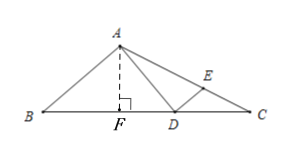
解:如图,过A作AF⊥BC,垂足为F,
∵AD⊥AB,
∴∠BAD =90°
在Rt△ABD中,由勾股定理得,
BD=![]() ,
,
∵AF⊥BD,
∴AF=![]() .
.
∵AD⊥AB,DE⊥AD,
∴∠BAD=∠ADE=90°,
∴AB∥DE,
∴∠CDE=∠B, ∠CED=∠CAB,
∴△CDE∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() ,
,
∴S△ADC=![]() .
.
故选:D

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目