题目内容
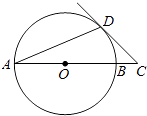
【题目】如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交 ![]() 于点D,点F是
于点D,点F是 ![]() 上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为 .
上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为 . 
【答案】36π﹣108
【解析】解:如图,∵CD⊥OA, ∴∠DCO=∠AOB=90°,
∵OA=OD=OB=6,OC= ![]() OA=
OA= ![]() OD,
OD,
∴∠ODC=∠BOD=30°,
作DE⊥OB于点E,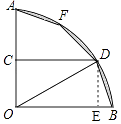
则DE= ![]() OD=3,
OD=3,
∴S弓形BD=S扇形BOD﹣S△BOD= ![]() ﹣
﹣ ![]() ×6×3=3π﹣9,
×6×3=3π﹣9,
则剪下的纸片面积之和为12×(3π﹣9)=36π﹣108,
所以答案是:36π﹣108.
【考点精析】本题主要考查了扇形面积计算公式的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
港口 | 运费(元/台) | |
甲库 | 乙库 | |
A港 | 14 | 20 |
B港 | 10 | 8 |
(1)设从甲仓库运送到A港口的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明费用最低时的调配方案.