题目内容
【题目】定义函数f（x），当x≤3时，f（x）=x2﹣2x，当x＞3时，f（x）=x2﹣10x+24，若方程f（x）=2x+m有且只有两个实数解，则m的取值范围为 ．
【答案】m＞﹣3或﹣12＜m＜﹣4
【解析】解：∵x≤3时，f（x）=x2﹣2x=（x﹣1）2﹣1， ∴该抛物线的顶点坐标为（1，﹣1），
当f（x）=0时，由x2﹣2x=0得x=0或x=2，
∴抛物线与x轴的交点为（0，0）和（2，0），
∵x＞3时，f（x）=x2﹣10x+24=（x﹣5）2﹣1，
∴此时抛物线的顶点坐标为（5，﹣1），
当f（x）=0时，由x2﹣10x+24=0得x=4或x=6，
∴此时抛物线与x轴的交点为（4，0）和（6，0），
由 
可得 
，即两抛物线交点坐标为（3，3），
如图所示：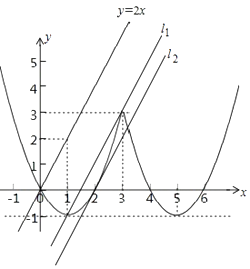
直线f（x）=2x+m可看作直线y=2x平移得到，
①当直线f（x）=2x+m过点（3，3），即6+m=3，得m=﹣3时，
直线f（x）=2x+m与f（x）=x2﹣2x的图象有两个交点；
②当直线f（x）=2x+m与f（x）=x2﹣2x有一个交点，即x2﹣2x=2x+m只有一个解时，方程f（x）=2x+m有且只有两个解，
解得：m=﹣4，
当直线f（x）=2x+m与f（x）=x2﹣10x+24只有1个交点时，即2x+m=x2﹣10x+24只有一个解，
解得：m=﹣12，
由图象可知当m＞﹣3或﹣12＜m＜﹣4时，方程f（x）=2x+m有且只有两个实数解，
所以答案是：m＞﹣3或﹣12＜m＜﹣4．
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案，需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
