��Ŀ����
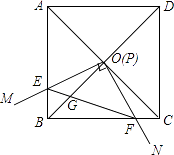
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����A���� ![]() ��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���x2��2x��3=0��������
��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���x2��2x��3=0��������
��1�����߶�BC�ij��ȣ�
��2�����ʣ�ֱ��AC��ֱ��AB�Ƿ�ֱ����˵�����ɣ�
��3������D��ֱ��AC�ϣ���DB=DC����ֱ��BD�Ľ���ʽ��
��4����x�����Ƿ����P��ʹ��O��B��P����Ϊ��������������ABC���ƣ������ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����x2��2x��3=0�ã�
��x1=3��x2=��1
��B��0��3����C��0����1����
��BC=4��
��2��
�⣺���ۣ�AC��AB���������£�
��A�� ![]() ��0����B��0��3����C��0����1����
��0����B��0��3����C��0����1����
��OA= ![]() ��OB=3��OC=1��
��OB=3��OC=1��
��tan��ABO= ![]() =
= ![]() ��tan��ACO=
��tan��ACO= ![]() =
= ![]() ��
��
���ABO=30�㣬��ACO=60�㣬
���BAC=90�㣬
��AC��AB
��3��
�⣺��ͼ1�У���D��DE��x����E��
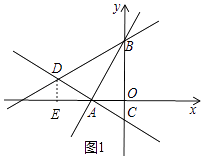
���DEA=��AOC=90�㣬
��tan��ACO= ![]() =
= ![]() ��
��
�ߡ�DCB=60��
��DB=DC��
���DBC�ǵȱ������Σ�
��BA��DC��
��DA=AC��
�ߡ�DAE=��OAC��
���ADE�ա�ACO��
��DE=OC=1��AE=OA= ![]()
�� ![]() ��
��
��D�������� ![]() ��1����
��1����
��ֱ��BD�Ľ���ʽΪy=kx+b������ ![]() ���
��� 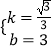 ��
��
��ֱ��BD�Ľ���ʽΪy= ![]() x+3
x+3
��4��
�⣺���ڣ���ͼ2�У��ӳ�BD��x����P1��
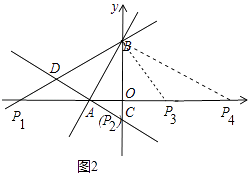
�ɣ�3����֪����DBC�ǵȱ������Σ�
���P1BO=60�㣬
���ڡ�ABC�У���ACB=60�㣬��CAB=90�㣬
���P1BC=��ACB=60�㣬�ߡ�P1OB=��CAB=90�㣬
���P1BO�ס�BCA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��OP1=3 ![]() ��
��
��P1����3 ![]() ��0����
��0����
��P2��A�غ�ʱ����BOP2�ס�BAC����ʱP2���� ![]() ��0����
��0����
�ٸ��ݶԳ��Կɵ�P3�� ![]() ��0����P4��3
��0����P4��3 ![]() ��0��Ҳ����������
��0��Ҳ����������
������������P����������3 ![]() ��0����
��0���� ![]() ��0����
��0���� ![]() ��0����3
��0����3 ![]() ��0��
��0��
����������1���з��̼��������B��C���������⣮��2����tan��ABO= ![]() =
= ![]() ��tan��ACO=
��tan��ACO= ![]() =
= ![]() ���Ƴ���ABO=30�㣬��ACO=60�㣬���ɽ�����⣮��3����ͼ1�У���D��DE��x����E���ɡ�ADE�ա�ACO���Ƴ�DE=OC=1��AE=OA=
���Ƴ���ABO=30�㣬��ACO=60�㣬���ɽ�����⣮��3����ͼ1�У���D��DE��x����E���ɡ�ADE�ա�ACO���Ƴ�DE=OC=1��AE=OA= ![]() �������D���꣬���ô���ϵ�������ɽ�����⣮��4�����ڣ���ͼ2�У��ӳ�BD��x����P1 �� ����֤��P1������������P2��A�غ�ʱҲ�����������ٸ��ݶԳ���д��P3��P4���꼴�ɣ�
�������D���꣬���ô���ϵ�������ɽ�����⣮��4�����ڣ���ͼ2�У��ӳ�BD��x����P1 �� ����֤��P1������������P2��A�غ�ʱҲ�����������ٸ��ݶԳ���д��P3��P4���꼴�ɣ�
�����㾫����������Ĺؼ���������һ�κ��������ʵ����֪ʶ������һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С���Լ���һ�κ�����ͼ������ʵ����⣬�˽�һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ��

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�